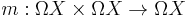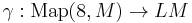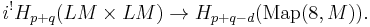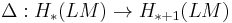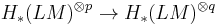String topology
String topology, a branch of mathematics, is the study of algebraic structures on the homology of free loop spaces. The field was started by Chas and Sullivan in 1999 (see Chas & Sullivan 1999).
Contents |
Motivation
While the singular cohomology of a space has always a product structure, this is not true for the singular homology of a space. Nevertheless, it is possible to construct such a structure for an oriented manifold M of dimension d. This is the so-called intersection product. Intuitively, one can describe it as follows: given classes 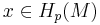 and
and 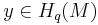 , take their product
, take their product 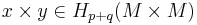 and make it transversal to the diagonal
and make it transversal to the diagonal 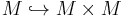 . The intersection is then a class in
. The intersection is then a class in 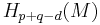 , the intersection product of x and y. One way to make this construction rigorous is to use stratifolds.
, the intersection product of x and y. One way to make this construction rigorous is to use stratifolds.
Another case, where the homology of a space has a product, is the (based) loop space 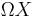 of a space X. Here the space itself has a product
of a space X. Here the space itself has a product
by going first the first loop and then the second. There is no analogous product structure for the free loop space LX of all maps from 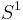 to X since the two loops need not have a common point. A substitute for the map m is the map
to X since the two loops need not have a common point. A substitute for the map m is the map
where Map(8, M) is the subspace of  , where the value of the two loops coincides at 0 and
, where the value of the two loops coincides at 0 and  is defined again by composing the loops. (Here "8" denotes the topological space "figure 8", i.e. the wedge of two circles.)
is defined again by composing the loops. (Here "8" denotes the topological space "figure 8", i.e. the wedge of two circles.)
The Chas–Sullivan product
The idea of the Chas–Sullivan product is to now combine in some way the product structures above. Consider two classes 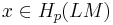 and
and 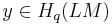 . Their product
. Their product 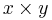 lies in
lies in 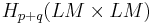 . We need a map
. We need a map
One way to construct this is to use stratifolds (or another geometric definition of homology) to do transversal intersection (after interpreting 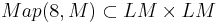 as an inclusion of Hilbert manifolds). Another approach starts with the collapse map from LM x LM to the Thom space of the normal bundle of Map(8, M). Composing the induced map in homology with the Thom isomorphism, we get the map we want.
as an inclusion of Hilbert manifolds). Another approach starts with the collapse map from LM x LM to the Thom space of the normal bundle of Map(8, M). Composing the induced map in homology with the Thom isomorphism, we get the map we want.
Now we can compose i! with the induced map of  to get a class in
to get a class in 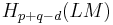 , the Chas–Sullivan product of x and y (see eg Cohen & Jones 2002).
, the Chas–Sullivan product of x and y (see eg Cohen & Jones 2002).
Remarks
- As in the case of the intersection product, there are different sign conventions concerning the Chas–Sullivan product. In some convention, it is graded commutative, in some it is not.
- The same construction works if we replace
 by another multiplicative homology theory h if M is oriented with respect to h.
by another multiplicative homology theory h if M is oriented with respect to h.
- Furthermore, we can replace LM by
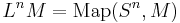 . By an easy variation of the above construction, we get that
. By an easy variation of the above construction, we get that 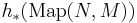 is a module over
is a module over 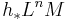 if N is a manifold of dimensions n.
if N is a manifold of dimensions n.
- The Serre spectral sequence is compatible with the above algebraic structures for both the fiber bundle
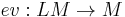 with fiber
with fiber 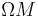 and the fiber bundle
and the fiber bundle 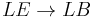 for a fiber bundle
for a fiber bundle 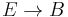 , which is important for computations (see Cohen&Jones&Yan2004 and Meier2010).
, which is important for computations (see Cohen&Jones&Yan2004 and Meier2010).
The Batalin-Vilkovisky structure
There is an action 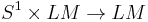 by rotation, which induces a map
by rotation, which induces a map
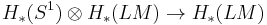 .
.
Plugging in the fundamental class ![[S^1]\in H_1(S^1)](/2012-wikipedia_en_all_nopic_01_2012/I/6e913a176e3e389de056296264d54471.png) , gives an operator
, gives an operator
of degree 1. One can show that this operator interacts nicely with the Chas–Sullivan product in the sense that they form together the structure of a Batalin-Vilkovisky algebra on 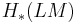 . This operator tends to be difficult to compute in general.
. This operator tends to be difficult to compute in general.
Field Theories
There are several attempts to construct (topological) field theories via string topology. The basic idea is to fix an oriented manifold M and associate to every surface with p incoming and q outgoing boundary components (with 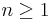 ) an operation
) an operation
which fulfills the usual axioms for a topological field theory. The Chas–Sullivan product is associated to the pair of pants. It can be shown that these operations are 0 if the genus of the surface is greater than 0 (see Tamanoi2010)
A more structured approach (exhibited in Godin2008) gives 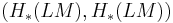 the structure of a degree d open-closed homological conformal field theory (HCFT) with positive boundary. Ignoring the open-closed part, this amounts to the following structure: let S be a surface with boundary, where the boundary circles are labeled as incoming or outcoming. If there are p incoming and q outgoing and
the structure of a degree d open-closed homological conformal field theory (HCFT) with positive boundary. Ignoring the open-closed part, this amounts to the following structure: let S be a surface with boundary, where the boundary circles are labeled as incoming or outcoming. If there are p incoming and q outgoing and 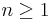 , we get operations
, we get operations
parametrized by a certain twisted homology of the mapping class group of S.
References
- M. Chas & D. Sullivan, String Topology, arXiv:math/9911159v1 (1999)
- R. Cohen & J. Jones, A homotopy theoretic realization of string topology, Mathematische Annalen 324, p. 773–798 (2002)
- R. Cohen & J. Jones & J. Yan, The loop homology algebra of spheres and projective spaces in Categorical decomposition techniques in algebraic topology: International Conference in Algebraic Topology, Isle of Skye, Scotland, June 2001, Birkhäuser, p. 77–92 (2004).
- L. Meier, Spectral Sequences in String Topology, arXiv:1001.4906v2 (2010)
- V. Godin, Higher string topology operations, arXiv:0711.4859v2 (2008)
- H. Tamanoi, Loop coproducts in string topology and triviality of higher genus TQFT operations , Journal of Pure and Applied Algebra 214, Issue 5 pp. 605-615 (2010)