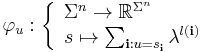String kernel

A string kernel is a mathematical tool used in large scale data analysis and mining, where sequence data are to be clustered or classified (concerning especially the popular research fields of text and gene analysis[1]). Kernels are often used in with support vector machines to transform data from its original space to one where it can be more easily separated and grouped. This may enable non-linear classification.

Contents

Informal Introduction

Suppose one wants to compare some text passages automatically and indicate their relative similarity. For many applications, it might be sufficient to find some keywords which match exactly. One example where exact matching is not always enough is found in spam detection[2]; another would be in computational gene analysis, where homologous genes have mutated, resulting in common subsequences along with deleted, inserted or replaced symbols.

Motivation

Since several well-proven data clustering, classification and information retrieval methods (for example support vector machines) are designed to work on vectors (i.e. data are elements of a vector space), using a string kernel allows the extension of these methods to handle sequence data.

The string kernel method is to be contrasted with earlier approaches for text classification where feature vectors only indicated the presence or absence of a word. Not only does it improve on these approaches, but it is an example for a whole class of kernels adapted to data structures, which began to appear at the turn of the 21st century. A survey of such methods has been compiled by Gärtner.[3]

Definition

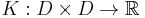A kernel on a domain D is a function K: D \times D \rightarrow \mathbb{R} satisfying some conditions (being symmetric in the arguments, continuous and positive semidefinite in a certain sense).

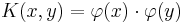Mercer's theorem asserts that K can then be expressed as K(x,y)=\varphi(x)\cdot \varphi(y) with \varphi mapping the arguments into an inner product space.

We can now reproduce the definition of a string subsequence kernel[4] on strings over an alphabet \Sigma. Coordinate-wise, the mapping is defined as follows:

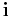\varphi_u�: \left\{ \begin{array}{l} \Sigma^n \rightarrow \mathbb{R}^{\Sigma^n} \\ s \mapsto \sum_{\mathbf{i}�: u=s_{\mathbf{i}}} \lambda^{l(\mathbf{i})} \end{array} \right.

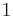The \mathbf{i} are multiindices and u is a string of length n: subsequences can occur in a non-contiguous manner, but gaps are penalized. The parameter \lambda may be set to any value between 0 (gaps are not allowed) and 1 (even widely-spread "occurrences" are weighted the same as appearances as a contiguous substring).

For several relevant algorithms, data enters into the algorithm only in expressions involving an inner product of feature vectors, hence the name kernel methods. A desirable consequence of this is that one does not need to explicitly calculate the transformation 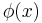\phi(x), only the inner product via the kernel, which may be a lot quicker, especially when approximated.[4]

References

  1. ^ Leslie, C.; Eskin, E.; Noble, W.S. (2002), The spectrum kernel: A string kernel for SVM protein classification, 7, pp. 566–575 
  2. ^ Amayri, O., Improved Online Support Vector Machines Spam Filtering Using String Kernels 
  3. ^ Gärtner, T. (2003), "A survey of kernels for structured data", CM SIGKDD Explorations Newsletter (ACM) 5 (1): 58 
  4. ^ a b Lodhi, Huma; Saunders, Craig; Shawe-Taylor, John; Cristianini, Nello; Watkins, Chris (2002), "Text classification using string kernels", The Journal of Machine Learning Research (MIT Press): 444