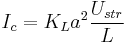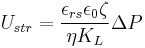Streaming current

A streaming current and streaming potential are two interrelated electrokinetic phenomena studied in the areas of surface chemistry and electrochemistry. They are an electric current or potential which originates when an electrolyte is driven by a pressure gradient through a channel or porous plug with charged walls.^[1]^[2]^[3]

The first observation of the streaming potential is generally attributed to the German physicist Georg Hermann Quincke in 1859.

1 Applications
2 Origin of the streaming current
3 Measurement method
4 Literature
5 References

Applications

Streaming currents in well-defined geometries are a sensitive method to characterize the zeta potential of surfaces, which is important in the fields of colloid and interface science.^[1] In geology, measurements of related spontaneous potential are used for evaluations of formations. Streaming potential has to be considered in design for flow of poorly conductive fluids (e.g., gasoline lines) because of the danger of buildup of high voltages. They could in principle be used to generate electrical power, however this process has not been applied so far because of its low efficiency.

Origin of the streaming current

Adjacent to the channel walls, the charge-neutrality of the liquid is violated due to the presence of the electrical double layer: a thin layer of counterions attracted by the charged surface.^[1]^[4]

The transport of counterions along with the pressure-driven fluid flow gives rise to a net charge transport: the streaming current. The reverse effect, generating a fluid flow by applying a potential difference, is called electroosmotic flow.^[4]^[5]^[6]

Measurement method

A typical setup to measure streaming currents consists of two reversible electrodes placed on either side of a fluidic geometry across which a known pressure difference is applied. When both electrodes are held at the same potential, the streaming current is measured directly as the electric current flowing through the electrodes. Alternatively, the electrodes can be left floating, allowing a streaming potential to build up between the two ends of the channel.

A streaming potential is defined as positive when the electric potential is higher on the high pressure end of the flow system that on the low pressure end.

The value of streaming current observed in a capillary is usually related to the zeta potential through the relation:^[7]

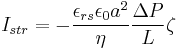$I_{str}=-\frac{\epsilon_{rs}\epsilon_0 a^2}{\eta} \frac{\Delta P}{L} \zeta$ .

The conduction current, which is equal in magnitude to the streaming current at steady state, is:

$I_c= K_L a^2 \frac{U_{str}}{L}$

At steady state, the streaming potential built up across the flow system is given by:

$U_{str}= \frac{\epsilon_{rs}\epsilon_0 \zeta}{\eta K_L} \Delta P$

Symbols:

I_str - streaming current under short-circuit conditions, A
U_str - streaming potential at zero net current conditions, V
I_c - conduction current, A
ε_rs - relative permittivity of the liquid, dimensionless
ε₀ - electrical permittivity of vacuum, F·m⁻¹
η - dynamic viscosity of the liquid, kg·m⁻¹·s⁻¹
ζ - zeta potential, V
ΔP - pressure difference, Pa
L - capillary length, m
a - capillary radius, m
K_L - specific conductivity of the bulk liquid, S·m⁻¹

The equation above is usually referred to as the Helmholtz-Smoluchowski equation.

The above equations assume that:

the double layer is not too large compared to the pores or capillaries (i.e., 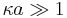$\kappa a \gg 1$ ), where κ is the reciprocal of the Debye length
there is no surface conduction (which typically may become important when the zeta potential is large, e.g., |ζ| > 50 mV)
there is no electrical double layer polarization
the surface is homogeneous in properties^[8]
there is not axial concentration gradient
the geometry is that of a capillary/tube.

Literature

J. Lyklema, Fundamentals of Interface and Colloid Science
F.H.J. van der Heyden et al., Phys. Rev. Lett. 95, 116104 (2005)
C. Werner et al., J. Colloid Interface Sci. 208, 329 (1998)

References

^ ^a ^b ^c Lyklema, J. (1995). Fundamentals of Interface and Colloid Science. Academic Press.
^ Li, D. (2004). Electrokinetics in Microfluidics. Academic Press.
^ Chang, H.C., Yeo, L. (2009). Electrokinetically Driven Microfluidics and Nanofluidics. Cambridge University Press.
^ ^a ^b Kirby, B.J. (2010). Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices.. Cambridge University Press. ISBN 978-0521119030. http://www.kirbyresearch.com/textbook.
^ Bruus, H. (2007). Theoretical Microfluidics. Oxford University Press.
^ Karniadakis, G.M., Beskok, A., Aluru, N. (2005). Microflows and Nanoflows. Springer Verlag.
^ ”Measurement and Interpretation of Electrokinetic Phenomena”, International Union of Pure and Applied Chemistry, Technical Report, published in Pure Appl.Chem., vol 77, 10, pp.1753-1805, 2005 (pdf).
^ Menachem Elimelech and Amy E. Childress, "ZETA POTENTIAL OF REVERSE OSMOSIS MEMBRANES: IMPLICACATIONS FOR MEMBRANE PERFORMANCE". U.S. DEPARTMENT OF THE INTERIOR, Bureau of Reclamation, Denver Office. Water Treatment Technology Program Report No. 10. December 1996.