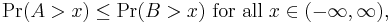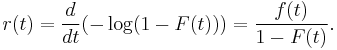Stochastic ordering
In probability theory and statistics, a stochastic order quantifies the concept of one random variable being "bigger" than another. These are usually partial orders, so that one random variable  may be neither stochastically greater than, less than nor equal to another random variable
may be neither stochastically greater than, less than nor equal to another random variable  . Many different orders exist, which have different applications.
. Many different orders exist, which have different applications.
Contents |
Usual stochastic order
A real random variable  is less than a random variable
is less than a random variable  in the "usual stochastic order" if
in the "usual stochastic order" if
where 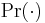 denotes the probability of an event. This is sometimes denoted
denotes the probability of an event. This is sometimes denoted 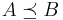 or
or 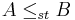 . If additionally
. If additionally 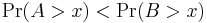 for some
for some  , then
, then  is stochastically strictly less than
is stochastically strictly less than  , sometimes denoted
, sometimes denoted 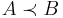 .
.
Characterizations
The following rules describe cases when one random variable is stochastically less than or equal to another. Strict version of some of these rules also exist.
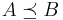 if and only if for all non-decreasing functions
if and only if for all non-decreasing functions  ,
, ![{\rm E}[u(A)] \le {\rm E}[u(B)]](/2012-wikipedia_en_all_nopic_01_2012/I/26c5840733f731d0c12e91e557fc65d6.png) .
.- If
 is non-decreasing and
is non-decreasing and 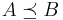 then
then 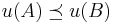
- If
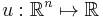 is an increasing function and
is an increasing function and 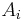 and
and 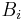 are independent sets of random variables with
are independent sets of random variables with 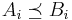 for each
for each  , then
, then 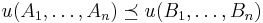 and in particular
and in particular 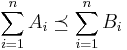 Moreover, the
Moreover, the  th order statistics satisfy
th order statistics satisfy 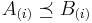 .
. - If two sequences of random variables
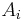 and
and 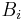 , with
, with 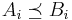 for all
for all  each converge in distribution, then their limits satisfy
each converge in distribution, then their limits satisfy 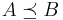 .
. - If
 ,
,  and
and  are random variables such that
are random variables such that 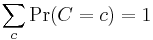 and
and 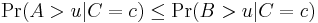 for all
for all  and
and  such that
such that 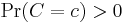 , then
, then 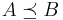 .
.
Other properties
If 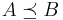 and
and ![{\rm E}[A]={\rm E}[B]](/2012-wikipedia_en_all_nopic_01_2012/I/b70a5aa8a4310fe6e41756173808965e.png) then
then 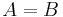 in distribution.
in distribution.
Stochastic dominance
Stochastic dominance[1] is a stochastic ordering used in decision theory. Several "orders" of stochastic dominance are defined.
- Zeroth order stochastic dominance consists of simple inequality:
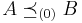 if
if 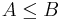 for all states of nature.
for all states of nature. - First order stochastic dominance is equivalent to the usual stochastic order above.
- Higher order stochastic dominance is defined in terms of integrals of the distribution function.
- Lower order stochastic dominance implies higher order stochastic dominance.
Multivariate stochastic order
Other stochastic orders
Hazard rate order
The hazard rate of a non-negative random variable  with absolutely continuous distribution function
with absolutely continuous distribution function  and density function
and density function  is defined as
is defined as
Given two non-negative variables  and
and  with absolutely continuous distribution
with absolutely continuous distribution  and
and  , and with hazard rate functions
, and with hazard rate functions  and
and  , respectively,
, respectively,  is said to be smaller than
is said to be smaller than  in the hazard rate order (denoted as
in the hazard rate order (denoted as 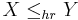 ) if
) if
 for all
for all 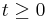 ,
,
or equivalently if
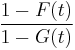 is decreasing in
is decreasing in  .
.
Likelihood ratio order
Let  and
and  two continuous (or discrete) random variables with densities (or discrete densities)
two continuous (or discrete) random variables with densities (or discrete densities) 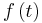 and
and 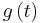 , respectively, so that
, respectively, so that 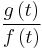 increases in
increases in  over the union of the supports of
over the union of the supports of  and
and  ; in this case,
; in this case,  is smaller than
is smaller than  in the likelihood ratio order (
in the likelihood ratio order (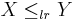 ).
).
Mean residual life order
Variability orders
If two variables have the same mean, they can still be compared by how "spread out" their distributions are. This is captured to a limited extent by the variance, but more fully by a range of stochastic orders.
Convex order
Convex order is a special kind of variability order. Under the convex ordering,  is less than
is less than  if and only if for all convex
if and only if for all convex  ,
, ![{\rm E}[u(A)] < {\rm E}[u(B)]](/2012-wikipedia_en_all_nopic_01_2012/I/024f2a6235e46c542b317a9d9c9b3de2.png) .
.
Laplace transform order
Laplace transform order is a special case of convex order where  is an exponential function:
is an exponential function: 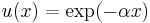 . Clearly, two random variables that are convex ordered are also Laplace transform ordered. The converse is not true.
. Clearly, two random variables that are convex ordered are also Laplace transform ordered. The converse is not true.
References
- M. Shaked and J. G. Shanthikumar, Stochastic Orders and their Applications, Associated Press, 1994.
- E. L. Lehmann. Ordered families of distributions. The Annals of Mathematical Statistics, 26:399–419, 1955.