Steinitz exchange lemma

The Steinitz exchange lemma is a basic theorem in linear algebra used, for example, to show that any two bases for a finite-dimensional vector space have the same number of elements. The result is named after the German mathematician Ernst Steinitz. The result is often called the Steinitz–Mac Lane exchange lemma, also recognizing the generalization[1] by Saunders Mac Lane of Steinitz's lemma to matroids.[2]

Contents

Statement

If {v1, ..., vm} is a set of m linearly independent vectors in a vector space V, and {w1, ..., wn} span V then m ≤ n and, possibly after reordering the wi, the set {v1, ..., vm, wm + 1, ..., wn} spans V.

Proof

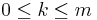We are going to show that for any integer k satisfying 0\leq k\leq m, the following assertion is valid:

(1) we have 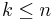k\leq n, and the set 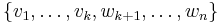\{ v_1,\ldots, v_k,w_{k%2B1},\ldots,w_n\} spans V.

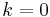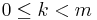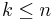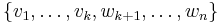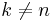In fact, we will prove (1) by induction over k: Being clear for k=0, the only thing that needs to be done is the induction step. So assume that some k satisfying 0\leq k<m is such that k\leq n and such that the set \{ v_1,\ldots, v_k,w_{k%2B1},\ldots,w_n\} spans V. 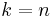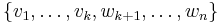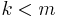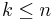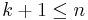Then, k\neq n (because otherwise, we would have k=n, so that the set \{ v_1,\ldots, v_k,w_{k%2B1},\ldots,w_n\} would be equal to the set \{ v_1,\ldots, v_k\}, but this set cannot span V since k<m and since the set \{ v_1,\ldots, v_m\} is linearly independent), and thus k\leq n can be sharpened to k%2B1\leq n.

Since 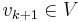v_{k%2B1}\in V, we may write 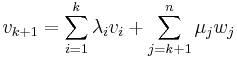v_{k%2B1}=\sum_{i=1}^k \lambda_i v_i%2B\sum_{j=k%2B1}^n \mu_j w_j. As also \{ v_1,\ldots,v_m \} are linearly independent not all the 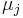\mu_j may be zero. Thus without loss of generality, by reordering the w, we may assume that 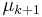\mu_{k%2B1} is not zero. Therefore, the equation 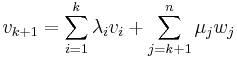v_{k%2B1}=\sum_{i=1}^k \lambda_i v_i%2B\sum_{j=k%2B1}^n \mu_j w_j can be used to write 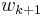w_{k%2B1} as a linear combination of 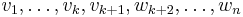v_1,\ldots ,v_k,v_{k%2B1},w_{k%2B2},\ldots ,w_n. In other words, 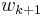w_{k%2B1} is in the span of 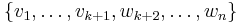\{ v_1,\ldots, v_{k%2B1},w_{k%2B2},\ldots,w_n\} and so the latter must be the whole of V. This completes the induction step, and (1) follows by induction on k. The Lemma now follows from (1), applied to k=m.

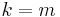Applications

The Steinitz exchange lemma is a basic result in computational mathematics, especially in linear algebra and in combinatorial algorithms.[3]

References

  1. ^ Mac Lane, Saunders (1936), "Some interpretations of abstract linear dependence in terms of projective geometry", American Journal of Mathematics (The Johns Hopkins University Press) 58 (1): 236–240, doi:10.2307/2371070, JSTOR 2371070 .
  2. ^ Kung, Joseph P. S., ed. (1986), A Source Book in Matroid Theory, Boston: Birkhäuser, ISBN 0-8176-3173-9, MR0890330 .
  3. ^ Page v in Stiefel: Stiefel, Eduard L. (1963). An introduction to numerical mathematics (Translated by Werner C. Rheinboldt & Cornelie J. Rheinboldt from the second German ed.). New York: Academic Press. pp. x+286. MR181077.