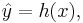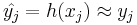Statistical classification
In machine learning, statistical classification is the problem of identifying the sub-population to which new observations belong, where the identity of the sub-population is unknown, on the basis of a training set of data containing observations whose sub-population is known. Therefore these classifications will show a variable behaviour which can be studied by statistics.
Thus the requirement is that new individual items are placed into groups based on quantitative information on one or more measurements, traits or characteristics, etc. and based on the training set in which previously decided groupings are already established.
The problem here may be contrasted with that for cluster analysis, where the problem is to analyse a single data-set and decide how and whether the observations in the data-set can be divided into groups. In certain terminology, particularly that of machine learning, the classification problem is known as supervised learning, while clustering is known as unsupervised learning.
Unfortunately, terminology can be different in various fields of application. For example, in community ecology, the term "classification" is synonymous with cluster analysis.
Contents |
Learning classifiers. Problem statement
A learning classifier is able to learn based on a sample. The data-set used for training consists of information x and y for each data-point, where x denotes what is generally a vector of observed characteristics for the data-item and y denotes a group-label. The label y can take only a finite number of values.
The classification problem can be stated as follows: given training data  produce a rule (or "classifier") h, such that h(x) can be evaluated for any possible value of x (not just those included in the training data) and such that the group attributed to any new observation, specifically
produce a rule (or "classifier") h, such that h(x) can be evaluated for any possible value of x (not just those included in the training data) and such that the group attributed to any new observation, specifically
is as close as possible to the true group label y. For the training data-set, the true labels yi are known but will not necessarily match their in-sample approximations
For new observations, the true labels yj are unknown, but it is a prime target for the classification procedure that the approximation
as well as possible, where the quality of this approximation needs to be judged on the basis of the statistical or probabilistic properties of the overall population from which future observations will be drawn.
Frequentist procedures
Early work on statistical classification was undertaken by Fisher,[1][2] in the context of two-group problems, leading to Fisher's linear discriminant function as the rule for assigning a group to a new observation.[3] This early work assumed that data-values within each of the two groups had a multivariate normal distribution. The extension of this same context to more than two-groups has also been considered with a restriction imposed that the classification rule should be linear.[3][4] Later work for the multivariate normal distribution allowed the classifier to be nonlinear:[5] several classification rules can be derived based on slight different adjustments of the Mahalanobis distance, with a new observation being assigned to the group whose centre has the lowest adjusted distance from the observation.
Bayesian procedures
Unlike frequentist procedures, Bayesian classification procedures provide a natural way of taking into account any available information about the relative sizes of the sub-populations associated with the different groups within the overall population.[6] Bayesian procedures tend to be computationally expensive and, in the days before Markov chain Monte Carlo computations were developed, approximations for Bayesian clustering rules were devised.[7]
Some Bayesian procedures involve the calculation of group membership probabilities: these can be viewed as providing a more informative outcome of a data analysis than a simple attribution of a single group-label to each new observation.
Binary and multiclass classification
Classification can be thought of as two separate problems - binary classification and multiclass classification. In binary classification, a better understood task, only two classes are involved, whereas in multiclass classification involves assigning an object to one of several classes.[8] Since many classification methods have been developed specifically for binary classification, multiclass classification often requires the combined use of multiple binary classifiers.
Algorithms
The most widely used classifiers are the neural network (multi-layer perceptron), support vector machines, k-nearest neighbours, Gaussian mixture model, Gaussian, naive Bayes, decision tree and RBF classifiers.
Examples of classification algorithms include:
- Linear classifiers
- Support vector machines
- Quadratic classifiers
- Kernel estimation
- Boosting
- Decision trees
- Neural networks
- Bayesian networks
- Hidden Markov models
- Learning vector quantization
Evaluation
Classifier performance depends greatly on the characteristics of the data to be classified. There is no single classifier that works best on all given problems (a phenomenon that may be explained by the no-free-lunch theorem). Various empirical tests have been performed to compare classifier performance and to find the characteristics of data that determine classifier performance. Determining a suitable classifier for a given problem is however still more an art than a science.
The measures precision and recall are popular metrics used to evaluate the quality of a classification system. More recently, receiver operating characteristic (ROC) curves have been used to evaluate the tradeoff between true- and false-positive rates of classification algorithms.
As a performance metric, the uncertainty coefficient has the advantage over simple accuracy in that it is not affected by the relative sizes of the different classes. [9] Further, it will not penalize an algorithm for simply rearranging the classes.
An intriguing problem in pattern recognition yet to be solved is the relationship between the problem to be solved (data to be classified) and the performance of various pattern recognition algorithms (classifiers).
Application domains
Classification problems has many applications. In some of these it is employed as a data mining procedure, while in others more detailed statistical modeling is undertaken.
- Computer vision
- Medical imaging and medical image analysis
- Optical character recognition
- Video tracking
- Drug discovery and development
- Geostatistics
- Speech recognition
- Handwriting recognition
- Biometric identification
- Biological classification
- Statistical natural language processing
- Document classification
- Internet search engines
- Credit scoring
- Pattern recognition
See also
References
- ^ Fisher R.A. (1936) " The use of multiple measurements in taxonomic problems", Annals of Eugenics, 7, 179–188
- ^ Fisher R.A. (1938) " The statistical utilization of multiple measurements", Annals of Eugenics, 8, 376–386
- ^ a b Gnanadesikan, R. (1977) Methods for Statistical Data Analysis of Multivariate Observations, Wiley. ISBN 0-471-30845-5 (p. 83–86)
- ^ Rao, C.R. (1952) Advanced Statistical Methods in Multivariate Analysis, Wiley. (Section 9c)
- ^ Anderson,T.W. (1958) An Introduction to Multivariate Statistical Analysis, Wiley.
- ^ Binder, D.A. (1978) "Bayesian cluster analysis", Biometrika, 65, 31–38.
- ^ Binder, D.A. (1981) "Approximations to Bayesian clustering rules", Biometrika, 68, 275–285.
- ^ Har-Peled, S., Roth, D., Zimak, D. (2003) "Constraint Classification for Multiclass Classification and Ranking." In: Becker, B., Thrun, S., Obermayer, K. (Eds) Advances in Neural Information Processing Systems 15: Proceedings of the 2002 Conference, MIT Press. ISBN 0262025507
- ^ Peter Mills (2011). "Efficient statistical classification of satellite measurements". International Journal of Remote Sensing. doi:10.1080/01431161.2010.507795.
External links
- Classifier showdown A practical comparison of classification algorithms.
- Statistical Pattern Recognition Toolbox for Matlab.
- TOOLDIAG Pattern recognition toolbox.
- Library of variable kernel density estimation routines written in C++..
- PAL Classification suite written in Java.
- kNN and Potential energy (Applet), University of Leicester