State-merging

In quantum information theory, quantum state merging (HOW05.I,HOW05.II) is the transfer of a quantum state when the receiver already has part of the state. The process optimally transfers partial information using entanglement and classical communication. 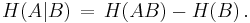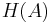It allows for sending information using an amount of entanglement given by the conditional quantum entropy, $H(A|B)\,=\,H(AB)-H(B) \, .$ with $H(A)$ the Von Neumann entropy, 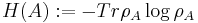$H(A):=-Tr\rho_A\log\rho_A$ . It thus provides an operational meaning to this quantity.

Unlike its classical counterpart, the quantum conditional entropy can be negative. In this case, the sender can transfer the state to the receiver using no entanglement, and as an added bonus, this amount of entanglement can be gained, rather than used. Thus quantum information can be negative.

The amount of classical information needed is the mutual information 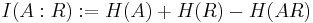$I(A:R):=H(A)%2BH(R)-H(AR)$ . The case where the classical communication is replaced by quantum communication was considered in (ADHW09). This is known as the Fully Quantum Slepian-Wolf Theorem, since everything is sent down the quantum channel. A single-shot version of state merging was found by Berta (B10), and a multiparty single shot version was found in (DH10). The quantum discord has been interpreted using state merging (MD10).

References

HOW05.I Horodecki, M.; Oppenheim, J.; Winter, A. (2005). "Partial quantum information". Nature 436: 673–676. arXiv:quant-ph/0505062. doi:10.1038/nature03909.

HOW05.IIHorodecki, M.; Oppenheim, J.; Winter, A. (2005). "Quantum state merging and negative information". Communications of Mathematical Physics 269: 107–136. arXiv:quant-ph/0512247. doi:80.1007/s00220-006-0118-x.

ADHW09Abeyesinghe, A.; Devetak, I.; Hayden, P; Winter, A. (2009). "The mother of all protocols: restructuring quantum information’s family tree". Proc. R. Soc. A 465: 2537–2563. arXiv:quant-ph. doi:10.1098/rspa.2009.0202.

B10 Berta, M. (2009). "Single-shot quantum state merging". arXiv:quant-ph/0912.4495.

DH10 Dutil, N.; Hayden, P. (2010). "One-shot Multiparty State Merging". arXiv:quant-ph/1011.1974.

MD10 Datta, A. (2010). "Interpreting quantum discord through quantum state merging". arXiv:quant-ph/1008.4135.