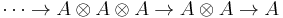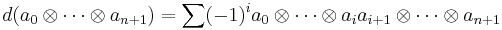Standard complex

Standard resolution redirects here, for the television monitor size, see standard definition

In mathematics, the standard complex, also called standard resolution, bar resolution, bar complex, bar construction, is a way of constructing resolutions in homological algebra. It was first introduced for the special case of algebras over a commutative ring by Eilenberg & Mac Lane (1953) and Cartan & Eilenberg (1956, IX.6) and has since been generalized in many ways.

The name "bar complex" comes from the fact that Eilenberg & Mac Lane (1953) used a vertical bar | as a shortened form of the tensor product ⊗ in their notation for the complex.

Contents

Definition

If A is an algebra over a field K, the standard complex is

\cdots\rightarrow A\otimes A\otimes A\rightarrow A\otimes A\rightarrow A

with the differential given by

d(a_0\otimes \cdots\otimes a_{n%2B1})=\sum (-1)^i a_0\otimes\cdots\otimes a_ia_{i%2B1}\otimes\cdots\otimes a_{n%2B1}

Normalized standard complex

The normalized (or reduced) standard complex replaces A⊗A⊗...⊗A⊗A with A⊗(A/K)⊗...⊗(A/K)⊗A.

Monads

See also

References