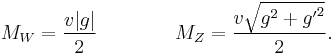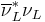Standard Model (mathematical formulation)
| Quantum field theory |
|---|
| History of... |
|
Incomplete theories
|
|
Scientists
Adler • Bethe • Bogoliubov • Callan • Candlin • Coleman • DeWitt • Dirac • Dyson • Fermi • Feynman • Fierz • Fröhlich • Gell-Mann • Goldstone • Gross • 't Hooft • Jackiw • Klein • Landau • Lee • Lehmann • Majorana • Nambu • Parisi • Polyakov • Salam • Schwinger • Skyrme • Stueckelberg • Symanzik • Tomonaga • Veltman • Weinberg • Weisskopf • Wilson • Witten • Yang • Yukawa • Hoodbhoy • Zimmermann • Zinn-Justin
|
- For a basic description, see the article on the Standard Model.
This is a detailed description of the standard model (SM) of particle physics. It describes how the leptons, quarks, gauge bosons and the Higgs particle fit together. It gives an outline of the main physics that the theory describes, and new directions in which it is moving.
It may be helpful to read this article along with the companion overview of the standard model.
Contents |
A chiral gauge theory
The chirality projections of a Dirac field ψ are
-
- "Left" chirality: ψL = ½(1 - γ5)ψ
- "Right" chirality: ψR = ½(1 + γ5)ψ
where γ5 is the fifth gamma matrix.
These are needed because the SM is a chiral gauge theory, i.e., the two helicities are treated differently.
This article uses the Dirac basis instead of the Weyl basis for describing spinors. The Weyl basis is more convenient because there is no natural correspondence between the left-handed and right-handed fermion fields other than that generated dynamically through the Yukawa couplings after the Higgs field has acquired a vacuum expectation value (VEV). In consulting common texts on the standard model one should expect to find the Weyl basis used.
Right handed singlets, left handed doublets
Under the weak isospin SU(2) the left-handed and right-handed chiralities have different charges. The left-handed particles are weak-isospin doublets (2), whereas the right-handed are singlets (1). The right-handed neutrino does not exist in the standard model. (However, in some extensions of the standard model it does.) The up-type quarks are charge 2/3 quarks: u, c, t. The charge -1/3 quarks (d, s, b) are called down-type quarks. The charged leptons (e, μ, τ) are denoted by l, and their corresponding neutrinos by ν. The theory contains
-
- the left handed doublet of quarks QL = (uL, dL) and leptons EL = (νlL, lL)
- the right handed singlets of quarks uR and dR and the charged leptons lR.
When the Standard Model was written down, there was no evidence for neutrino mass. Now, however, a series of experiments including Super-Kamiokande have indicated that neutrinos indeed have a tiny mass. This fact can be simply accommodated in the Standard Model by adding a right-handed neutrino. This, however, is not strictly necessary. For example, the dimension 5 operator 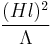 also leads to neutrino oscillations.
also leads to neutrino oscillations.
This pattern is replicated in the next generations. We introduce a generation label i = 1,2,3 and write ui to denote the three generations of up-type quarks, and similarly for the down type quarks. The left-handed quark doublet also carries a generation index, QiL, as does the lepton doublet, EiL.
Why this?
What dictates this form of the weak isospin charges? The coupling of a right-handed neutrino to matter in weak interactions was ruled out by experiment long ago. Benjamin Lee and J. Zinn-Justin, and Gerardus 't Hooft and Martinus Veltman in 1972 suggested the inclusion of left and right-handed fields into the same multiplet. This possibility has been ruled out by experiment. This leaves the construction given above.
For the leptons, the gauge group can then be SU(2)l × U(1)L × U(1)R. The two U(1) factors can be combined into U(1)Y × U(1)l where l is the lepton number. Gauging of the lepton number is ruled out by experiment, leaving only the possible gauge group SU(2)L × U(1)Y. A similar argument in the quark sector also gives the same result for the electroweak theory. This form of the theory developed from a suggestion by Sheldon Glashow in 1961 and extended independently by Steven Weinberg and Abdus Salam in 1967 (and was anticipated in rudimentary form by Julian Schwinger in 1957).
The gauge field part
The gauge group has already been described. Now one needs the fields. The correct kinetic term for a spin-1 field with local gauge invariance is built from the (non-Abelian) field strength tensor
in terms of the gauge field 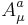 , where the subscript
, where the subscript  runs over spacetime dimensions (0 to 3) and the superscript
runs over spacetime dimensions (0 to 3) and the superscript  over the elements of the adjoint representation of the gauge group, and
over the elements of the adjoint representation of the gauge group, and  is the gauge coupling constant. The quantity
is the gauge coupling constant. The quantity 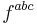 is the structure constant of the gauge group, defined by the commutator
is the structure constant of the gauge group, defined by the commutator ![[t_{a}, t_{b}] = f^{abc} t_{c}](/2012-wikipedia_en_all_nopic_01_2012/I/1f34340ba667daee3274e6846f30948b.png) . In an Abelian group, since the generators
. In an Abelian group, since the generators 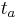 all commute with each other, the structure constants vanish, and the field tensor takes its usual Abelian form.
all commute with each other, the structure constants vanish, and the field tensor takes its usual Abelian form.
We need to introduce three gauge fields corresponding to each of the subgroups 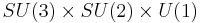 —
—
- The gluon field tensor will be denoted by
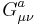 , where the index
, where the index  labels elements of the 8 representation of colour SU(3). The strong coupling constant will be labelled
labels elements of the 8 representation of colour SU(3). The strong coupling constant will be labelled 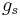 or
or  , the former where there is any ambiguity. The observations leading to the discovery of this part of the SM are discussed in the article in quantum chromodynamics.
, the former where there is any ambiguity. The observations leading to the discovery of this part of the SM are discussed in the article in quantum chromodynamics. - The notation
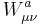 will be used for the gauge field tensor of SU(2) where a runs over the 3 generators of this group. The coupling will always be denoted by
will be used for the gauge field tensor of SU(2) where a runs over the 3 generators of this group. The coupling will always be denoted by  . The gauge field will be denoted by
. The gauge field will be denoted by 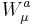 .
. - The gauge field tensor for the U(1) of weak hypercharge will be denoted by
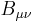 , the coupling by
, the coupling by 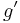 , and the gauge field by
, and the gauge field by 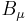 .
.
The Gauge Field Lagrangian
Using the field strength tensors, the kinetic terms for the electroweak gauge fields are
The standard model Lagrangian consists of another similar term constructed using the gluon field tensor.
The W, Z and photon
The charged W bosons are the linear combinations
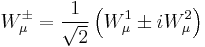 .
.
Z bosons (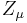 ) and photons (
) and photons (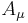 ) are mixtures of
) are mixtures of 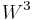 and
and  . The precise mixture is determined by the Weinberg angle
. The precise mixture is determined by the Weinberg angle 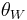 :
:
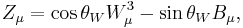 and
and 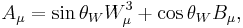
with 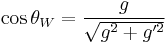 .
.
The electric charge Q, weak isospin T3 (aka Tz) and weak hypercharge YW are related by
Note: usually weak hypercharge is scaled so that
which is a formally equivalent to Gell-Mann–Nishijima formula.
The charged and neutral current couplings
The charged currents 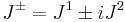 are
are
These charged currents are precisely those that entered the Fermi theory of beta decay. The action contains the charge current piece
It will be discussed later in this article that the W boson becomes massive, and for energy much less than this mass, the effective theory becomes the current-current interaction of the Fermi theory.
However, gauge invariance now requires that the component 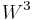 of the gauge field also be coupled to a current that lies in the triplet of SU(2). However, this mixes with the U(1), and another current in that sector is needed. These currents must be uncharged in order to conserve charge. So we require the neutral currents
of the gauge field also be coupled to a current that lies in the triplet of SU(2). However, this mixes with the U(1), and another current in that sector is needed. These currents must be uncharged in order to conserve charge. So we require the neutral currents
The neutral current piece in the Lagrangian is then
There are no mass terms for the fermions. Everything else will come through the scalar (Higgs) sector.
Quantum chromodynamics
Leptons carry no colour charge; quarks do. Moreover, the quarks have only vector couplings to the gluons, i.e., the two helicities are treated on par in this part of the standard model. So the coupling term is given by
Here Ta stands for the generators of SU(3) colour. The mass term in QCD arises from interactions in the Higgs sector.
The Higgs field
One requires masses for the W, Z, quarks and leptons. Recent experiments have also shown that the neutrino has a mass. However, the details of the mechanism that give the neutrinos a mass are not yet clear. So this article deals with the classic version of the SM (circa 1990s, when neutrino masses could be neglected with impunity).
The Yukawa terms
Giving a mass to a Dirac field requires a term in the Lagrangian that couples the left and right helicities. A complex scalar doublet (charge 2) Higgs field, 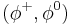 is introduced, which couples through the Yukawa interaction
is introduced, which couples through the Yukawa interaction
where 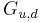 are 3×3 matrices of Yukawa couplings, with the ij term giving the coupling of the generations i and j.
are 3×3 matrices of Yukawa couplings, with the ij term giving the coupling of the generations i and j.
Symmetry breaking
The Higgs part of the Lagrangian is
where 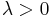 and
and 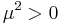 , so that the mechanism of spontaneous symmetry breaking can be used.
, so that the mechanism of spontaneous symmetry breaking can be used.
In a unitarity gauge one can set 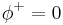 and make
and make 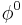 real. Then
real. Then 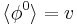 is the non-vanishing vacuum expectation value of the Higgs field. Putting this into
is the non-vanishing vacuum expectation value of the Higgs field. Putting this into  , a mass term for the fermions is obtained, with a mass matrix
, a mass term for the fermions is obtained, with a mass matrix 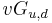 . From
. From 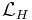 , quadratic terms in
, quadratic terms in 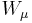 and
and 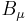 arise, which give masses to the W and Z bosons
arise, which give masses to the W and Z bosons
Including neutrino mass
As mentioned earlier, in the SM classic there are no right-handed neutrinos. The same mechanism as the quarks would then give masses to the electrons, but because of the missing right-handed neutrino the neutrinos remain massless. Small changes can also accommodate massive neutrinos. Two approaches are possible—
- Add
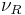 , and give a mass term as usual (this is called a Dirac mass)
, and give a mass term as usual (this is called a Dirac mass) - Write a Majorana mass term by combining
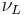 with its complex conjugate
with its complex conjugate
See seesaw mechanism.
These alternatives can easily lead beyond the SM.
The GIM mechanism and the CKM matrix
The Yukawa couplings for the quarks are not required to have any particular symmetry, so they cannot be diagonalized by unitary transformations. However, they can be diagonalized by separate unitary matrices acting on the two sides (this process is called a singular value decomposition). In other words one can find diagonal matrices
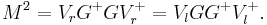 ::
::
This matrix V is called the Cabibbo-Kobayashi-Maskawa (CKM) matrix. The matrix is usually not diagonal, and therefore causes mixing of the quark flavours. It also gives rise to CP-violations in the SM.
See also
- Overview of standard model of particle physics
- Weak interactions, Fermi theory of beta decay and electroweak theory
- Strong interactions, flavour, quark model and quantum chromodynamics
- For open questions, see quark matter, CP violation and neutrino masses
- noncommutative standard model
- Beyond the Standard Model
- Weinberg angle
- Electroweak interaction
- Fundamental interaction
References and external links
- The quantum theory of fields (vol 2), by S. Weinberg (Cambridge University Press, 1996) ISBN 0-521-55002-5.
- Gauge theory of elementary particle physics, by T.P. Cheng and L.F. Li (Oxford University Press, 1982) ISBN 0-19-851961-3.
- An introduction to quantum field theory, by M.E. Peskin and D.V. Schroeder (HarperCollins, 1995) ISBN 0-201-50397-2.
- PDF, PostScript, and LaTeX version of the Standard Model Lagrangian with explicit Higgs terms
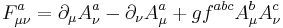
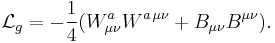
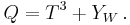
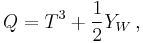
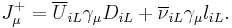
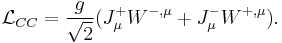
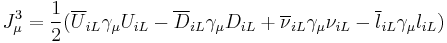
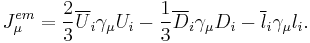
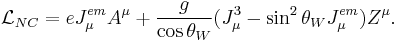
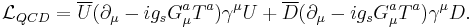
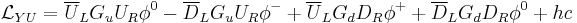
![\mathcal{L}_H = [(\partial_\mu -ig W_\mu^a t^a -ig'Y_{\phi} B_\mu)\phi]^2 %2B \mu^2 \phi^\dagger\phi-\lambda (\phi^\dagger\phi)^2,](/2012-wikipedia_en_all_nopic_01_2012/I/d591ed1e5e9f091443831457f7135b6e.png)