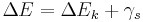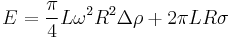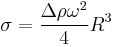Spinning drop method
Spinning drop method (rotating drop method) is one of the methods that is used to measure interfacial tension. Basically, measurements are carried out in a rotating horizontal tube which contains a dense fluid. One drop of a less dense liquid is placed inside the fluid. Since the rotation of the horizontal tube creates a centrifugal force towards the tube walls, the liquid drop starts to be elongated and this elongation stops when the interfacial tension and centrifugal forces are balanced. Values obtained at this equilibrium point are used to estimate surface tension of the particular liquid by using appropriate correlations. A device called “spinning drop tensiometer” is generally utilized for this purpose.
Spinning drop method is usually preferred for the accurate measurements of surface tensions below 10−2 mN/m. This is because of the limitations in the correlations where a sufficient elongation of the liquid is required. It refers to either using the fluids with low interfacial tension or working at very high angular velocities. This method is widely used in many different applications such as measuring the interfacial tension of polymer blends[1] and copolymers.[2]
Contents |
Theory
An approximate theory was developed by Bernard Vonnegut[3], in 1942, to measure the surface tension of the fluids, which is based on the principle that the interfacial tension and centrifugal forces are balanced at mechanical equilibrium. In the theory, shape of the liquid drop at the equilibrium is assumed as a circular cylinder.
The relation between the surface tension and angular velocity can be obtained in different ways. One of them is considering the total energy change in liquid drop as the summation of the change in kinetic energy and the surface energy:
The terms in the equation can be replaced by the total kinetic energy change between the stationary fluid and the fluid with an angular velocity, ω, and the surface energy of the circular cylinder that has a length, L, and radius, R:
where Δρ is the difference in fluid densities, and σ is the interfacial tension. At mechanical equilibrium, the energy change in radial direction has to be minimum. Differentiating the energy equation with respect to R, and solving for σ yields:
This equation is known as Vonnegut’s expression. Interfacial tension of any liquid that gives a shape very close to a cylinder at the equilibrium point, can be estimated using this equation.
New developments after 1942
The full mathematical analysis on the shape of spinning drops was done by Princen and others.[4] Progress in numerical algorithms and available computing resources turned solving the non linear implicit parameter equations to a pretty much 'common' task, which has been tackled by various authors and companies. The results are proving the Vonnegut restriction is no longer valid for the spinning drop method.
Comparison with other methods
Spinning drop method facilitates the measurement of surface tension compared to other widely used methods. Because in this method, measuring the contact angle is not required between a solid surface and the liquid. Another advantage of the method is that, it is not necessary to estimate the curvature at the interface, which usually brings difficulties with taking the first and second derivatives describing the shape of the fluid drop.
On the other hand, this theory suggested by Vonnegut, is restricted with the rotational velocity. Spinning drop method is not expected to give accurate results for the high surface tension measurements, since the centrifugal force that is required to maintain a cylindrical shape of the drop is much higher in the case of liquids that has high interfacial tensions.
References
- ^ H.H. Hu, D.D. Joseph (1994). "Evolution of a Liquid Drop in a spinning Drop Tensiometer". J. Colloid Interface Sci. 162 (2): 331–339. doi:10.1006/jcis.1994.1047.
- ^ C. Verdier, H.T.M. Vinagre, M. Piau, D.D. Joseph (2000). "High temperature interfacial tension measurements of PA6/PP interfaces compatibilized with copolymers using a spinning drop tensiometer". Polymer 41 (17): 6683–6689. doi:10.1016/S0032-3861(00)00059-8.
- ^ B. Vonnegut (1942). "Rotating Bubble Method for the Determination of Surface and Interfacial Tensions". Rev. Sci. Instrum. 13 (6): 6–9. doi:10.1063/1.1769937.
- ^ Princen, H; Zia, I; Mason, S (1967). "Measurement of Interfacial Tension from the Shape of a Rotating Drop". Journal of Colloid and Interface Science 23: 99. doi:10.1016/0021-9797(67)90090-2.