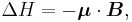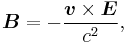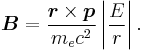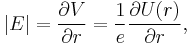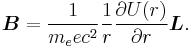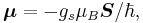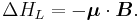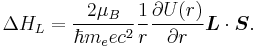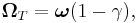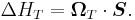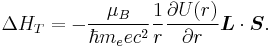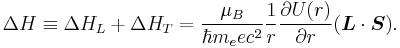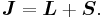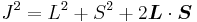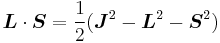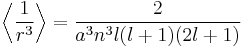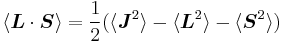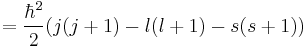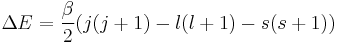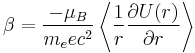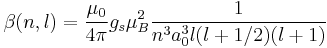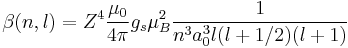Spin–orbit interaction
In quantum physics, the spin–orbit interaction (also called spin–orbit effect or spin–orbit coupling) is any interaction of a particle's spin with its motion. The first and best known example of this is that spin-orbit interaction causes shifts in an electron's atomic energy levels due to electromagnetic interaction between the electron's spin and the nucleus's magnetic field. This is detectable as a splitting of spectral lines. A similar effect, due to the relationship between angular momentum and the strong nuclear force, occurs for protons and neutrons moving inside the nucleus, leading to a shift in their energy levels in the nucleus shell model. In the field of spintronics, spin-orbit effects for electrons in semiconductors and other materials are explored and put to useful work.
Contents |
Spin–orbit interaction in atomic energy levels
Using some semiclassical electrodynamics and non-relativistic quantum mechanics, in this section we present a relatively simple and quantitative description of the spin-orbit interaction for an electron bound to an atom, up to first order in perturbation theory. This gives results that agree reasonably well with observations. A more rigorous derivation of the same result would start with the Dirac equation, and achieving a more precise result would involve calculating small corrections from quantum electrodynamics.
Energy of a magnetic moment
The energy of a magnetic moment in a magnetic field is given by:
where μ is the magnetic moment of the particle and B is the magnetic field it experiences.
Magnetic field
We shall deal with the magnetic field first. Although in the rest frame of the nucleus, there is no magnetic field, there is one in the rest frame of the electron. Ignoring for now that this frame is not inertial, in SI units we end up with the equation
where v is the velocity of the electron and E the electric field it travels through. Now we know that E is radial so we can rewrite 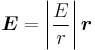 . Also we know that the momentum of the electron
. Also we know that the momentum of the electron 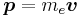 . Substituting this in and changing the order of the cross product gives:
. Substituting this in and changing the order of the cross product gives:
Next, we express the electric field as the gradient of the electric potential 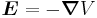 . Here we make the central field approximation, that is, that the electrostatic potential is spherically symmetric, so is only a function of radius. This approximation is exact for hydrogen, and indeed hydrogen-like systems. Now we can say
. Here we make the central field approximation, that is, that the electrostatic potential is spherically symmetric, so is only a function of radius. This approximation is exact for hydrogen, and indeed hydrogen-like systems. Now we can say
where 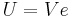 is the potential energy of the electron in the central field, and e is the elementary charge. Now we remember from classical mechanics that the angular momentum of a particle
is the potential energy of the electron in the central field, and e is the elementary charge. Now we remember from classical mechanics that the angular momentum of a particle 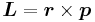 . Putting it all together we get
. Putting it all together we get
It is important to note at this point that B is a positive number multiplied by L, meaning that the magnetic field is parallel to the orbital angular momentum of the particle.
Magnetic Moment of the Electron
The magnetic moment of the electron is
where 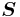 is the spin angular momentum vector,
is the spin angular momentum vector, 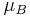 is the Bohr magneton and
is the Bohr magneton and 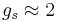 is the electron spin g-factor. Here,
is the electron spin g-factor. Here, 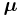 is a negative constant multiplied by the spin, so the magnetic moment is antiparallel to the spin angular momentum.
is a negative constant multiplied by the spin, so the magnetic moment is antiparallel to the spin angular momentum.
The spin-orbit potential consists of two parts. The Larmor part is connected to interaction of the magnetic moment of electron with magnetic field of nucleus in the co-moving frame of electron. The second contribution is related to Thomas precession.
Larmor interaction energy
The Larmor interaction energy is
Substituting in this equation expressions for the magnetic moment and the magnetic field, one gets
Now, we have to take into account Thomas precession correction for the electron's curved trajectory.
Thomas interaction energy
In 1926 Llewellyn Thomas relativistically recomputed the doublet separation in the fine structure of the atom.[1]. Thomas precession rate, 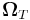 , is related to the angular frequency of the orbital motion,
, is related to the angular frequency of the orbital motion, 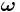 , of a spinning particle as follows [2][3]
, of a spinning particle as follows [2][3]
where  is the Lorentz factor of moving particle. The Hamiltonian producing the spin precession
is the Lorentz factor of moving particle. The Hamiltonian producing the spin precession 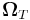 is given by
is given by
To the first order in 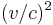 , we obtain
, we obtain
Total interaction energy
The total spin-orbit potential in an external electrostatic potential takes the form
The net effect of Thomas precession is the reduction of the Larmor interaction energy by factor 1/2 which came to be known as the Thomas half.
Evaluating the energy shift
Thanks to all the above approximations, we can now evaluate the detailed energy shift in this model. In particular, we wish to find a basis that diagonalizes both H0 (the non-perturbed Hamiltonian) and ΔH. To find out what basis this is, we first define the total angular momentum operator
Taking the dot product of this with itself, we get
(since L and S commute), and therefore
It can be shown that the five operators H0, J², L², S², and Jz all commute with each other and with ΔH. Therefore, the basis we were looking for is the simultaneous eigenbasis of these five operators (i.e., the basis where all five are diagonal). Elements of this basis have the five quantum numbers: n (the "principal quantum number") j (the "total angular momentum quantum number"), l (the "orbital angular momentum quantum number"), s (the "spin quantum number"), and jz (the "z-component of total angular momentum").
To evaluate the energies, we note that
for hydrogenic wavefunctions (here 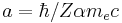 is the Bohr radius divided by the nuclear charge Z); and
is the Bohr radius divided by the nuclear charge Z); and
Final Energy Shift
We can now say
where
For hydrogen, we can write the explicit result
For any hydrogen-like atom with Z protons
See also
References
- ^ L. H. Thomas, The motion of the spinning electron, Nature (London), 117, 514 (1926).
- ^ L. Föppl and P. J. Daniell, Zur Kinematik des Born'schen starren Körpers, Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 519 (1913).
- ^ C. Møller, The Theory of Relativity, (Oxford at the Claredon Press, London, 1952).
Textbooks
- E. U. Condon and G. H. Shortley (1935). The Theory of Atomic Spectra. Cambridge University Press. ISBN 0-521-09209-4.
- D. J. Griffiths (2004). Introduction to Quantum Mechanics (2nd edition). Prentice Hall.
- Landau, Lev; L. M. Lifshitz. "
 72. Fine structure of atomic levels". Quantum Mechanics: Non-Relativistic Theory, Volume 3.
72. Fine structure of atomic levels". Quantum Mechanics: Non-Relativistic Theory, Volume 3.