Reflection theorem

For reflection principles in set theory, see reflection principle.

In algebraic number theory, a reflection theorem or Spiegelungssatz (German for reflection theorem – see Spiegel and Satz) is one of a collection of theorems linking the sizes of different ideal class groups (or ray class groups), or the sizes of different isotypic components of a class group. The original example is due to Ernst Eduard Kummer, who showed that the class number of the cyclotomic field 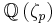$\mathbb{Q} \left( \zeta_p \right)$ , with p a prime number, will be divisible by p if the class number of the maximal real subfield 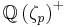$\mathbb{Q} \left( \zeta_p \right)^{%2B}$ is. Another example is due to Scholz^[1]. 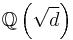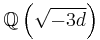A simplified version of his theorem states that if 3 divides the class number of a real quadratic field $\mathbb{Q} \left( \sqrt{d} \right)$ , then 3 also divides the class number of the imaginary quadratic field $\mathbb{Q} \left( \sqrt{-3d} \right)$ .

Both of the above results are generalized by Leopoldt's "Spiegelungssatz", which relates the p-ranks of different isotypic components of the class group of a number field K, considered as a module over the Galois group of a Galois extension K/k. Extensions of his Spiegelungssatz were given by Oriat and Oriat-Satge, where class groups were no longer associated with characters of the Galois group of K/k, but rather by ideals in a group ring over the Galois group of K/k. Leopoldt's Spiegelungssatz was generalized in a different direction by Kuroda, who extended it to a statement about ray class groups. This was further developed into the very general "T-S reflection theorem" of Georges Gras^[2]. Kenkichi Iwasawa also provided an Iwasawa-theoretic reflection theorem.

Notes

^ A. Scholz, Uber die Beziehung der Klassenzahlen quadratischer Korper zueinander, J. reine angew. Math., 166 (1932), 201-203.
^ Georges Gras, Class Field Theory: From Theory to Practice, Springer-Verlag, Berlin, 2004, pp. 157–158.