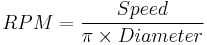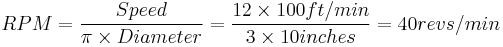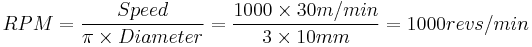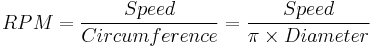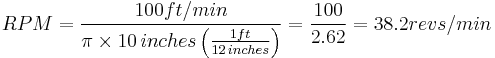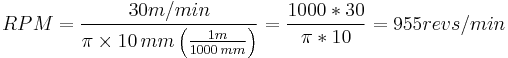Speeds and feeds

The phrase speeds and feeds (or feeds and speeds) refers to two separate velocities in machine tool practice, cutting speed and feed rate. They are often considered as a pair because of their combined effect on the cutting process. Each, however, can also be considered and analyzed in its own right.

Cutting speed (also called surface speed or simply speed) is the speed difference (relative velocity) between the cutting tool and the surface of the workpiece it is operating on. It is expressed in units of distance along the workpiece surface per time, typically surface feet per minute (sfm) or meters per minute (m/min).[1] Feed rate (also often styled as a solid compound, feedrate, or called simply feed) is the relative velocity at which the cutter is advanced along the workpiece; its vector is perpendicular to the vector of cutting speed. Feed rate units depend on the motion of the tool and workpiece; in rotating systems (e.g., turning and boring), the units are almost always distance per spindle revolution (inches per revolution [in/rev or ipr] or millimeters per revolution [mm/rev]).[2] In linear systems (e.g., milling), the units are typically distance per time (inches per minute [in/min or ipm] or millimeters per minute [mm/min]), although distance per revolution or per cutter tooth are also sometimes used.[2]

If variables such as cutter geometry and the rigidity of the machine tool and its tooling setup could be ideally maximized (and reduced to negligible constants), then only a lack of power (that is, kilowatts or horsepower) available to the spindle would prevent the use of the maximum possible speeds and feeds for any given workpiece material and cutter material. Of course, in reality those other variables are dynamic and not negligible; but there is still a correlation between power available and feeds and speeds employed. In practice, lack of rigidity is usually the limiting constraint.

The phrases "speeds and feeds" or "feeds and speeds" have sometimes been used metaphorically to refer to the execution details of a plan, which only skilled technicians (as opposed to designers or managers) would know.

Contents

Cutting speed

Cutting speed may be defined as the rate (or speed) that the material moves past the cutting edge of the tool , irrespective of the machining operation used – the surface speed. A cutting speed for mild steel, of 100 ft/min (or approx 30 meters/min) is the same whether it is the speed of the (stationary) cutter passing over the (moving) workpiece, such as in a turning operation, or the speed of the (rotating) cutter moving past a (stationary) workpiece, such as in a milling operation. What will affect the value of this surface speed for mild steel, is the cutting conditions:

For a given material there will be an optimum cutting speed for a certain set of machining conditions, and from this speed the spindle speed (RPM) can be calculated. Factors affecting the calculation of cutting speed are:

Cutting speeds are calculated on the assumption that optimum cutting conditions exist, these include:

The cutting speed is given as a set of constants that are available from the material manufacturer or supplier, the most common materials are available in reference books, or charts but will always be subject to adjustment depending on the cutting conditions. The following table gives the cutting speeds for a selection of common materials under one set of conditions. The conditions are a tool life of 1 hour, dry cutting (no coolant) and at medium feeds so they may appear to be incorrect depending on circumstances. These cutting speeds may change if, for instance, adequate coolant is available or an improved grade of HSS is used (such as one that includes cobalt).

Cutting speeds for various materials using a plain high speed steel cutter
Material type Meters per min (MPM) Surface feet per min (SFM)
Steel (tough) 15–18 50–60
Mild steel 30–38 100–125
Cast iron (medium) 18–24 60–80
Alloy steels (1320–9262) 20-37 65–120[3]
Carbon steels (C1008-C1095) 21-40 70–130[4]
Free cutting steels (B1111-B1113 & C1108-C1213) 35-69 115–225[4]
Stainless steels (300 & 400 series) 23-40 75–130[5]
Bronzes 24–45 80–150
Leaded steel (Leadloy 12L14) 91 300[6]
Aluminium 75–105 250–350
Brass 90-210 300-700[7] (Max. spindle speed)[8]

Machinability rating

Main article: Machinability

The machinability rating of a material attempts to quantify the machinability of various materials. It is expressed as a percentage or a normalized value. The American Iron and Steel Institute (AISI) determined machinability ratings for a wide variety of materials by running turning tests at 180 surface feet per minute (sfpm). It then arbitrarily assigned 160 Brinell B1112 steel a machinability rating of 100%. The machinability rating is determined by measuring the weighed averages of the normal cutting speed, surface finish, and tool life for each material. Note that a material with a machinability rating less than 100% would be more difficult to machine than B1112 and material with a value more than 100% easier.

Machinability ratings can be used in conjunction with the Taylor tool life equation, 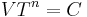VT^n = C, in order to determine cutting speeds or tool life. It is known that B1112 has a tool life of 60 minutes at a cutting speed of 100 sfpm. If a material has a machinability rating of 70%, it can be determined, with the above knowns, that in order to maintain the same tool life (60 minutes) the cutting speed must be 70 sfpm (assuming the same tooling is used).

When calculating for other copper alloys the machine rating is arrived at by assuming the 100 rating of 600 SFM. For example, phosphorus bronze (grades A–D) has a machinability rating of 20. This means that phosphor bronze runs at 20% the speed of 600 SFM or 120 SFM. However, 165 SFM is generally accepted as the basic 100% rating for "grading steels".[9]

Spindle speed

The spindle speed is the rotational frequency of the spindle of the machine, measured in revolutions per minute (RPM). The preferred speed is determined by working backward from the desired surface speed (sfm or m/min) and incorporating the diameter (of workpiece or cutter).

The spindle may hold the:

Excessive spindle speed will cause premature tool wear, breakages, and can cause tool chatter, all of which can lead to potentially dangerous conditions. Using the correct spindle speed for the material and tools will greatly enhance tool life and the quality of the surface finish.

For a given machining operation, the cutting speed will remain constant for most situations; therefore the spindle speed will also remain constant. However, facing, forming, parting off, and recess operations on a lathe or screw machine involve the machining of a constantly changing diameter. Ideally this means changing the spindle speed as the cut advances across the face of the workpiece, producing constant surface speed (CSS). Mechanical arrangements to effect CSS have existed for centuries, but they were never applied commonly to machine tool control. In the pre-CNC era, the ideal of CSS was ignored for most work. For unusual work that demanded it, special pains were taken to achieve it. The introduction of CNC-controlled lathes has provided a practical, everyday solution via automated CSS. By means of the machine's software and variable speed electric motors, the lathe can increase the RPM of the spindle as the cutter gets closer to the center of the part.

Grinding wheels are designed to be run at a maximum safe speed, the spindle speed of the grinding machine may be variable but this should only be changed with due attention to the safe working speed of the wheel. As a wheel wears it will decrease in diameter, and its effective cutting speed will be reduced. Some grinders have the provision to increase the spindle speed which corrects for this loss of cutting ability, however increasing the speed beyond the wheels rating will destroy the wheel and create a serious hazard to life and limb.

Generally speaking, spindle speeds and feed rates are less critical in woodworking than metalworking. Most woodworking machines including power saws such as circular saws and band saws, jointers, Thickness planers rotate at a fixed RPM. In those machines, cutting speed is regulated through the feed rate. The required feed rate can be extremely variable depending on the power of the motor, the hardness of the wood or other material being machined, and the sharpness of the cutting tool.

In woodworking, the ideal feed rate is one that is slow enough not to bog down the motor, yet fast enough to avoid burning the material. Certain woods, such as black cherry and maple are more prone to burning than others. The right feed rate is usually obtained by "feel" if the material is hand fed, or by trial and error if a power feeder is used. In thicknessers (planers), the wood is usually fed automatically through rubber or corrugated steel rollers. Some of these machines allow varying the feed rate, usually by changing pulleys. A slower feed rate usually results in a finer surface as more cuts are made for any length of wood.

Spindle speed becomes important in the operation of routers, spindle moulders or shapers, and drills. Older and smaller routers often rotate at a fixed spindle speed, usually between 20,000 and 25,000 rpm. While these speeds are fine for small router bits, using larger bits, say more than 1-inch (25 mm) or 25 millimeters in diameter, can be dangerous and can lead to chatter. Larger routers now have variable speeds and larger bits require slower speed. Drilling wood generally uses higher spindle speeds than metal, and the speed is not as critical. However, larger diameter drill bits do require slower speeds to avoid burning.

Cutting feeds and speeds, and the spindle speeds that are derived from them, are the ideal cutting conditions for a tool. If the conditions are less than ideal then adjustments are made to the spindle's speed, this adjustment is usually a reduction in RPM to the closest available speed, or one that is deemed (through knowledge and experience) to be correct.

Some materials, such as machinable wax, can be cut at a wide variety of spindle speeds, while others, such as stainless steel require much more careful control as the cutting speed is critical, to avoid overheating both the cutter and workpiece. Stainless steel is one material that work hardens very easily, therefore insufficient feed rate or incorrect spindle speed can lead to less than ideal cutting conditions as the work piece will quickly harden and resist the tool's cutting action. The liberal application of cutting fluid can improve these cutting conditions however the correct selection of speeds is the critical factor.

Spindle speed calculations

Most metalworking books have nomograms or tables of spindle speeds and feed rates for different cutters and workpiece materials; similar tables are also likely available from the manufacturer of the cutter used.

The spindle speeds may be calculated for all machining operations once the SFM or MPM is known. In most cases we are dealing with a cylindrical object such as a milling cutter or a workpiece turning in a lathe so we need to determine the speed at the periphery of this round object. This speed at the periphery (of a point on the circumference, moving past a stationary point) will depend on the rotational speed (RPM) and diameter of the object.

One analogy would be a skateboard rider and a bicycle rider travelling side by side along the road. For a given surface speed (the speed of this pair along the road) the rotational speed (RPM) of their wheels (large for the skater and small for the bicycle rider) will be different. This rotational speed (RPM) is what we are calculating, given a fixed surface speed (speed along the road) and known values for their wheel sizes (cutter or workpiece).

The following formulae[10] may be used to estimate this value.

Approximation

The exact RPM is not always needed, a close approximation will work (using 3 for the value of 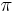{\pi }).

RPM = {Speed \over \pi \times Diameter}

e.g. for a cutting speed of 100 ft/min (a plain HSS steel cutter on mild steel) and diameter of 10 inches (the cutter or the work piece)

RPM = {Speed \over \pi \times Diameter} = {12 \times 100 ft/min \over 3 \times 10 inches} = {40 revs/min}

and, for an example using metric values, where the cutting speed is 30 m/min and a diameter of 10 mm,

RPM = {Speed \over \pi \times Diameter} = { 1000 \times 30 m/min \over 3 \times 10 mm} = {1000 revs/min}

Accuracy

However for more accurate calculations, and at the expense of simplicity, this formula can be used:

RPM = {Speed \over Circumference}={Speed \over \pi \times Diameter}

and using the same example as above

RPM = {100 ft/min \over \pi \times 10 \, inches \left ( \frac{1 ft}{12 \, inches} \right )} = {100 \over 2.62} = 38.2 revs/min

and using the same example as above

RPM = {30 m/min \over \pi \times 10 \, mm \left ( \frac{1 m}{1000 \, mm} \right )} = {1000*30 \over \pi*10} = 955 revs/min

where:

Feed rate

Feed rate is the velocity at which the cutter is fed, that is, advanced against the workpiece. It is expressed in units of distance per revolution for turning and boring (typically inches per revolution [ipr] or millimeters per revolution). It can be expressed thus for milling also, but it is often expressed in units of distance per time for milling (typically inches per minute [ipm] or millimeters per minute), with considerations of how many teeth (or flutes) the cutter has then determining what that means for each tooth.

Feedrate is dependent on the:

When deciding what feed rate to use for a certain cutting operation, the calculation is fairly straightforward for single-point cutting tools, because all of the cutting work is done at one point (done by "one tooth", as it were). With a milling machine or jointer, where multi-tipped/multi-fluted cutting tools are involved, then the desirable feed rate becomes dependent on the number of teeth on the cutter, as well as the desired amount of material per tooth to cut (expressed as chip load). The greater the number of cutting edges, the higher the feed rate permissible: for a cutting edge to work efficiently it must remove sufficient material to cut rather than rub; it also must do its fair share of work.

The ratio of the spindle speed and the feed rate controls how aggressive the cut is, and the nature of the swarf formed.

Formula to determine feed rate

This formula[11] can be used to figure out the feed rate that the cutter travels into or around the work. This would apply to cutters on a milling machine, drill press and a number of other machine tools. This is not to be used on the lathe for turning operations, as the feed rate on a lathe is given as feed per revolution.

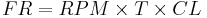
FR = {RPM \times T \times CL}

Where:

Depth of cut

Cutting speed and feed rate come together with depth of cut to determine the material removal rate, which is the volume of workpiece material (metal, wood, plastic, etc.) that can be removed per time unit.

Interrelationship of theory and practice

Speed-and-feed selection is analogous to other examples of applied science, such as meteorology or pharmacology, in that the theoretical modeling is necessary and useful but can never fully predict the reality of specific cases because of the massively multivariate environment. Just as weather forecasts or drug dosages can be modeled with fair accuracy, but never with complete certainty, machinists can predict with charts and formulas approximately which speed and feed values will work best on a particular job, but cannot know the exact optimal values until running the job. In CNC machining, usually the programmer programs speeds and feedrates that are as maximally tuned as calculations and general guidelines can supply. The operator then fine-tunes the values while running the machine, based on sights, sounds, smells, temperatures, tolerance holding, and tool tip lifespan. Under proper management, the revised values are captured for future use, so that when a program is run again later, this work need not be duplicated.

As with meteorology and pharmacology, however, the interrelationship of theory and practice has been evolving over decades as the theory part of the balance becomes more advanced thanks to information technology. For example, an effort called the Machine Tool Genome Project is working toward providing the computer modeling (simulation) needed to predict optimal speed-and-feed combinations for particular setups in any internet-connected shop with less local experimentation and testing.[12] Instead of the only option being the measuring and testing of the behavior of its own equipment, it will benefit from others' experience and simulation; in a sense, rather than 'reinventing a wheel', it will be able to 'make better use of existing wheels already developed by others in remote locations'.

Academic Researches

Flórez-Orrego et al.(2010) studied the effect of the variation of cutting parameters in the surface integrity in turning processing of an AISI 304 stainless steel. They found that the feed rate has the greatest impairing effect on the quality of the surface. Besides they found that, more than the achievement of the desired roughness profile, it should be analyized the effect on the creation of micropits and microdefects on the machined surface. Moreover, they found that the convectional empirical relation that relates the feed rate and the roughness value does not fit adequately for low cutting speeds. [1]

References

  1. ^ Smid 2008, pp. 74,85–90
  2. ^ a b Smid 2008, pp. 74,91–92
  3. ^ Brown & Sharpe, Automatic Screw Machine Handbook: Brown and Sharpe Speeds and Feeds Chart, p. 222 & 223
  4. ^ a b Brown & Sharpe, Automatic Screw Machine Handbook: Brown and Sharpe Speeds and Feeds Chart, p. 222
  5. ^ Brown & Sharpe, Automatic Screw Machine Handbook: Brown and Sharpe Speeds and Feeds Chart, p. 224
  6. ^ Brown & Sharpe, Cam & Tool Design: Surface Cutting Speeds Chart, p. 5
  7. ^ Speed/Feed Reference for Turning, Milling, and Drilling
  8. ^ Brown & Sharpe, Automatic Screw Machine Handbook: Brown and Sharpe Speeds and Feeds Chart, p. 226
  9. ^ Brown & Sharpe, Automatic Screw Machine Handbook: Machinebility of Materials, Composition and Machinability Chart, p. 120 & 224 – 225
  10. ^ Culley, Ron (1988). Fitting and machining. Melbourne, Victoria: RMIT Publications. ISBN 0724138196. 
  11. ^ Google Books: Feed Rate Equation
  12. ^ Zelinski 2011.

Bibliography

Further reading

External links

Introduction
Forms
List of woods
Tools
Other
Geometry
Other
Treatments
Woodworkers
Organizations
Category: Woodworking