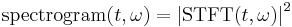Spectrogram

A spectrogram is a time-varying spectral representation[1] (forming an image) that shows how the spectral density of a signal varies with time. Also known as spectral waterfalls, sonograms, voiceprints, or voicegrams, spectrograms are used to identify phonetic sounds, to analyse the cries of animals; they were also used in many other fields including music, sonar/radar, speech processing,[2] seismology, etc. The instrument that generates a spectrogram is called a spectrograph and is equivalent to a sonograph.

Contents

Format

The most common format is a graph with two geometric dimensions: the horizontal axis represents time, the vertical axis is frequency; a third dimension indicating the amplitude of a particular frequency at a particular time is represented by the intensity or colour of each point in the image.

There are many variations of format: sometimes the vertical and horizontal axes are switched, so time runs up and down; sometimes the amplitude is represented as the height of a 3D surface instead of color or intensity. The frequency and amplitude axes can be either linear or logarithmic, depending on what the graph is being used for. Audio would usually be represented with a logarithmic amplitude axis (probably in decibels, or dB), and frequency would be linear to emphasize harmonic relationships, or logarithmic to emphasize musical, tonal relationships.

Generation

Spectrograms are usually created in one of two ways: approximated as a filterbank that results from a series of bandpass filters (this was the only way before the advent of modern digital signal processing), or calculated from the time signal using the short-time Fourier transform (STFT). These two methods actually form two different quadratic Time-Frequency Distributions, but are equivalent under some conditions.

The bandpass filters method usually uses analog processing to divide the input signal into frequency bands; the magnitude of each filter's output controls a transducer that records the spectrogram as an image on paper.[3]

Creating a spectrogram using the STFT is usually a digital process. Digitally sampled data, in the time domain, is broken up into chunks, which usually overlap, and Fourier transformed to calculate the magnitude of the frequency spectrum for each chunk. Each chunk then corresponds to a vertical line in the image; a measurement of magnitude versus frequency for a specific moment in time. The spectrums or time plots are then "laid side by side" to form the image or a three-dimensional surface.[4]

The spectrogram of a signal s(t) can be estimated by computing the squared magnitude of the STFT of the signal s(t), as follows:[5]

\mathrm{spectrogram}(t,\omega)=\left|\mathrm{STFT}(t,\omega)\right|^2

Applications

Limitations and resynthesis

From the formula above, it appears that a spectrogram contains no information about the exact phase of the signal that it represents. For this reason, it is not possible to reverse the process and generate a copy of the original signal from a spectrogram, though in situations where the exact initial phase is unimportant (of which audio may be one), it may be possible to generate a useful approximation of the original signal. The Analysis & Resynthesis Sound Spectrograph [1] is an example of a computer program that attempts to do this. In fact, there is some phase information in the spectrogram, but it appears in another form, as time delay (or group delay) which is the dual of the Instantaneous Frequency; an experiment explaining and relating these two concepts is described in[15]

See also

References

  1. ^ S. Haykin, editor, Advances in Spectrum Analysis and Array Processing, vol.1, Prentice-Hall, 1991.
  2. ^ JL Flanagan, Speech Analysis, Synthesis and Perception, Springer- Verlag, New York, 1972
  3. ^ Illustration of an electro-mechanical spectrograph
  4. ^ Spectrogram definition
  5. ^ STFT spectrogram details
  6. ^ Bird Songs and Spectrograms of Southern Tuscany
  7. ^ A wearable tactile sensory aid for profoundly deaf children
  8. ^ Spectrogram Reading
  9. ^ Praat - doing phonetics by computer
  10. ^ Several sound spectrogram examples, including the one by Aphex Twin
  11. ^ Example of using spectrograms to check filter responses
  12. ^ High definition spectrograms of common RF signals
  13. ^ Spectrograms for vector network analyzers
  14. ^ Real-time spectrogram displays from seismic stations
  15. ^ B. Boashash, "Estimating and Interpreting the Instantaneous Frequency of a Signal-Part I: Fundamentals", Proceedings of the IEEE, Vol. 80, No. 4, pp. 519-538, April 1992, doi:10.1109/5.135376

External links