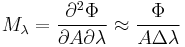Spectral power distribution
In color science and radiometry, a spectral power distribution (SPD) describes the power per unit area per unit wavelength of an illumination (radiant exitance), or more generally, the per-wavelength contribution to any radiometric quantity (radiant energy, radiant flux, radiant intensity, radiance, irradiance, radiant exitance, or radiosity).[1][2]
Mathematically, for the spectral power distribution of a radiant exitance or irradiance one may write:
where 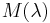 is the spectral irradiance (or exitance) of the light (SI units: W/m3 = kg/(m·s3));
is the spectral irradiance (or exitance) of the light (SI units: W/m3 = kg/(m·s3)); 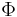 is the radiant flux of the source (SI unit: watt, W);
is the radiant flux of the source (SI unit: watt, W);  is the area over which the radiant flux is integrated (SI unit: square meter, m2); and
is the area over which the radiant flux is integrated (SI unit: square meter, m2); and  is the wavelength (SI unit: meter, m). (Note that it is more convenient to express the wavelength of light in terms of nanometers; spectral exitance would then be expressed in units of W·m−2·nm−1.) The approximation is valid when the area and wavelength interval are small.
is the wavelength (SI unit: meter, m). (Note that it is more convenient to express the wavelength of light in terms of nanometers; spectral exitance would then be expressed in units of W·m−2·nm−1.) The approximation is valid when the area and wavelength interval are small.
Relative SPD
Because the luminance of lighting fixtures and other light sources are handled separately, a spectral power distribution may be normalized in some manner, often to unity at 555 or 560 nanometers, coinciding with the peak of the eye's luminosity function.[2][3]
References
- ^ Mark D. Fairchild (2005). Color Appearance Models. John Wiley and Sons. ISBN 0470012161. http://books.google.com/books?id=8_TxzK2B-5MC&pg=PA56&dq=light+source+%22spectral+power+distribution%22&lr=&as_brr=3&ei=wgCJR6bHNpOMtAPpj6HQBQ&sig=dIlnEgPmXu9Sy3YpEVF6wy9m8tU#PPA57,M1.
- ^ a b Michael R. Peres (2007). The Focal Encyclopedia of Photography. Focal Press. ISBN 9780240807409. http://books.google.com/books?id=VYyldcYfq3MC&pg=RA1-PA383&dq=%22spectral+power+distribution%22+555+560+nm&lr=&as_brr=0&as_pt=ALLTYPES&ei=MdVTSaHNEJTckwSOpfQk.
- ^ Wyszecki, Günter; Stiles, Walter Stanley (1982). Color Science: Concepts and Methods; Quantitative Data and Formulae (second edition ed.). New York: Wiley. ISBN 978-0-471-39918-6.
External links
- Spectral Power Distribution Curves, GE Lighting.