Space hierarchy theorem
In computational complexity theory, the space hierarchy theorems are separation results that show that both deterministic and nondeterministic machines can solve more problems in (asymptotically) more space, subject to certain conditions. For example, a deterministic Turing machine can solve more decision problems in space n log n than in space n. The somewhat weaker analogous theorems for time are the time hierarchy theorems.
The foundation for the hierarchy theorems lies in the intuition that with either more time or more space comes the ability to compute more functions (or decide more languages). The hierarchy theorems are used to demonstrate that the time and space complexity classes form a hierarchy where classes with tighter bounds contain fewer languages than those with more relaxed bounds. Here we define and prove the space hierarchy theorem.
The space hierarchy theorems rely on the concept of space-constructible functions. The deterministic and nondeterministic space hierarchy theorems state that for all space-constructible functions f(n),
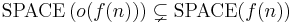 ,
,
where SPACE stands for either DSPACE or NSPACE.
Contents |
Statement
Formally, a function 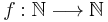 is space-constructible if
is space-constructible if 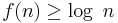 and there exists a Turing machine which computes the function
and there exists a Turing machine which computes the function 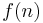 in space
in space 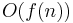 when starting with an input
when starting with an input 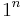 , where
, where 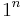 represents a string of
represents a string of 
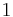 s. Most of the common functions that we work with are space-constructible, including polynomials, exponents, and logarithms.
s. Most of the common functions that we work with are space-constructible, including polynomials, exponents, and logarithms.
For every space-constructible function 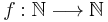 , there exists a language
, there exists a language  that is decidable in space
that is decidable in space 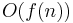 but not in space
but not in space 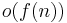 .
.
Proof
The goal here is to define a language that can be decided in space 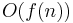 but not space
but not space 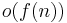 . Here we define the language
. Here we define the language  :
:
Now, for any machine  that decides a language in space
that decides a language in space 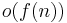 ,
,  will differ in at least one spot from the language of
will differ in at least one spot from the language of  , namely at the value of
, namely at the value of 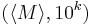 . The algorithm for deciding the language
. The algorithm for deciding the language  is as follows:
is as follows:
- On an input
 , compute
, compute 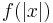 using space-constructibility, and mark off
using space-constructibility, and mark off 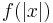 cells of tape. Whenever an attempt is made to use more than
cells of tape. Whenever an attempt is made to use more than 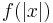 cells, reject.
cells, reject. - If
 is not of the form
is not of the form 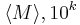 for some TM
for some TM  , reject.
, reject. - Simulate
 on input
on input  for at most
for at most 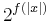 steps (using
steps (using 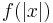 space). If the simulation tries to use more than
space). If the simulation tries to use more than 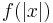 space or more than
space or more than 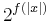 operations, then reject.
operations, then reject. - If
 accepted
accepted  during this simulation, then reject; otherwise, accept.
during this simulation, then reject; otherwise, accept.
Note on step 3: Execution is limited to 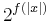 steps in order to avoid the case where
steps in order to avoid the case where  does not halt on the input
does not halt on the input  . That is, the case where
. That is, the case where  consumes space of only
consumes space of only 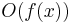 as required, but runs for infinite time.
as required, but runs for infinite time.
Comparison and improvements
The space hierarchy theorem is stronger than the analogous time hierarchy theorems in several ways:
- It only requires s(n) to be at least log n instead of at least n.
- It can separate classes with any asymptotic difference, whereas the time hierarchy theorem requires them to be separated by a logarithmic factor.
- It only requires the function to be space-constructible, not time-constructible.
It seems to be easier to separate classes in space than in time. Indeed, whereas the time hierarchy theorem has seen little remarkable improvement since its inception, the nondeterministic space hierarchy theorem has seen at least one important improvement by Viliam Geffert in his 2003 paper "Space hierarchy theorem revised". This paper made several striking generalizations of the theorem:
- It relaxes the space-constructibility requirement. Instead of merely separating the union classes DSPACE(O(s(n)) and DSPACE(o(s(n)), it separates DSPACE(f(n)) from DSPACE(g(n)) where f(n) is an arbitrary O(s(n)) function and g(n) is a computable o(s(n)) function. These functions need not be space-constructible or even monotone increasing.
- It identifies a unary language, or tally language, which is in one class but not the other. In the original theorem, the separating language was arbitrary.
- It does not require s(n) to be at least log n; it can be any nondeterministically fully space-constructible function.
Corollaries
Corollary 1
For any two functions 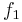 ,
, 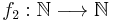 , where
, where 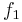 (n) is o(
(n) is o(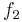 (n)) and
(n)) and 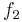 is space-constructible, SPACE(
is space-constructible, SPACE(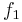 (n))
(n)) 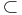 SPACE(
SPACE(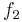 (n)).
(n)).
This corollary lets us separate various space complexity classes. For any function 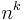 is space-constructible for any natural number k. Therefore for any two natural numbers
is space-constructible for any natural number k. Therefore for any two natural numbers 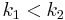 we can prove SPACE(
we can prove SPACE(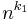 )
) 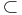 SPACE(
SPACE(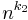 ). We can extend this idea for real numbers in the following corollary. This demonstrates the detailed hierarchy within the PSPACE class.
). We can extend this idea for real numbers in the following corollary. This demonstrates the detailed hierarchy within the PSPACE class.
Corollary 2
For any two real numbers 0 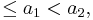 SPACE(
SPACE(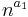 )
) 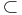 SPACE(
SPACE(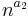 ).
).
Corollary 3
Proof
Savitch's theorem shows that NL 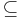 SPACE(
SPACE(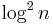 ), while the space hierarchy theorem shows that SPACE(
), while the space hierarchy theorem shows that SPACE(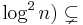 SPACE(
SPACE( ). Thus we get this corollary along with the fact that TQBF
). Thus we get this corollary along with the fact that TQBF 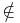 NL since TQBF is PSPACE-complete.
NL since TQBF is PSPACE-complete.
This could also be proven using the non-deterministic space hierarchy theorem to show that NL 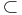 NPSPACE, and using Savitch's theorem to show that PSPACE = NPSPACE.
NPSPACE, and using Savitch's theorem to show that PSPACE = NPSPACE.
Corollary 4
This last corollary shows the existence of decidable problems that are intractable. In other words their decision procedures must use more than polynomial space.
Corollary 5
There are problems in PSPACE requiring an arbitrarily large exponent to solve; therefore PSPACE does not collapse to DSPACE(nk) for some constant k.
References
- Luca Trevisan. Notes on Hierarchy Theorems. Handout 7. CS172: Automata, Computability and Complexity. U.C. Berkeley. April 26, 2004.
- Viliam Geffert. Space hierarchy theorem revised. Theoretical Computer Science, volume 295, number 1-3, p.171-187. February 24, 2003.
- Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X. Pages 306–310 of section 9.1: Hierarchy theorems.
- Christos Papadimitriou (1993). Computational Complexity (1st edition ed.). Addison Wesley. ISBN 0-201-53082-1. Section 7.2: The Hierarchy Theorem, pp.143–146.