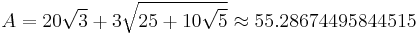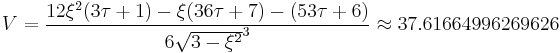Snub dodecahedron
| Snub dodecahedron | |
|---|---|
(Click here for rotating model) |
|
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 92, E = 150, V = 60 (χ = 2) |
| Faces by sides | (20+60){3}+12{5} |
| Schläfli symbol | s{5,3} |
| Wythoff symbol | | 2 3 5 |
| Coxeter-Dynkin | |
| Symmetry | I, [5,3]+, (532) |
| Dihedral Angle | |
| References | U29, C32, W18 |
| Properties | Semiregular convex chiral |
Colored faces |
3.3.3.3.5 (Vertex figure) |
Pentagonal hexecontahedron (dual polyhedron) |
Net |
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.
The snub dodecahedron has 92 faces (the most of any convex uniform polyhedron other than prisms and antiprisms), of which 12 are pentagons and the other 80 are equilateral triangles. It also has 150 edges, and 60 vertices. It has two distinct forms, which are mirror images (or "enantiomorphs") of each other.
Contents |
Geometric relations
The snub dodecahedron can be generated by taking the twelve pentagonal faces of the dodecahedron and pulling them outward so they no longer touch. At a proper distance this can create the rhombicosidodecahedron by filling in square faces between the divided edges and triangle faces between the divided vertices. But for the snub form, only add the triangle faces and leave the square gaps empty. Then apply an equal rotation to the centers of the pentagons and triangles, continuing the rotation until the gaps can be filled by two equilateral triangles.
Dodecahedron |
Rhombicosidodecahedron (Expanded dodecahedron) |
The snub dodecahedron can also be derived from the truncated icosidodecahedron by the process of alternation. Sixty of the vertices of the truncated icosidodecahedron form a polyhedron topologically equivalent to one snub dodecahedron; the remaining 60 form its mirror-image. The resulting polyhedron is vertex-transitive but not uniform, because its edges are of unequal lengths; some deformation is required to transform it into a uniform polyhedron.
Archimedes, an ancient Greek who showed major interest in polyhedral shapes, wrote a treatise on thirteen semi-regular solids. The snub dodecahedron is one of them.
Cartesian coordinates
Cartesian coordinates for the vertices of a snub dodecahedron are all the even permutations of
- (±2α, ±2, ±2β),
- (±(α+β/τ+τ), ±(-ατ+β+1/τ), ±(α/τ+βτ-1)),
- (±(-α/τ+βτ+1), ±(-α+β/τ-τ), ±(ατ+β-1/τ)),
- (±(-α/τ+βτ-1), ±(α-β/τ-τ), ±(ατ+β+1/τ)) and
- (±(α+β/τ-τ), ±(ατ-β+1/τ), ±(α/τ+βτ+1)),
with an even number of plus signs, where
- α = ξ-1/ξ
and
- β = ξτ+τ2+τ/ξ,
where τ = (1+√5)/2 is the golden ratio and ξ is the real solution to ξ3-2ξ=τ, which is the number:
![\xi = \sqrt[3]{\frac{\tau}{2} %2B \frac{1}{2}\sqrt{\tau - \frac{5}{27}}} %2B \sqrt[3]{\frac{\tau}{2} - \frac{1}{2}\sqrt{\tau - \frac{5}{27}}}](/2012-wikipedia_en_all_nopic_01_2012/I/159967f20c2df3f26365ea3651cfee6d.png)
or approximately 1.7155615.
This snub dodecahedron has an edge length of approximately 6.0437380841.
Taking the even permutations of the above coordinates with an odd number of plus signs gives another form, the enantiomorph of the other one.
Surface area and volume
For a snub dodecahedron whose edge length is 1, the surface area is
and the volume is
where τ is the golden ratio.
Snub dodecahedron has the highest sphericity of all Archimedean solids.
Related polyhedra and tilings
This semiregular polyhedron is a member of a sequence of snubbed polyhedra and tilings with vertex figure (3.3.3.3.p) and Coxeter-Dynkin diagram . These face-transitive figures have (n32) rotational symmetry.
(3.3.3.3.3) (332) |
(3.3.3.3.4) (432) |
(3.3.3.3.5) (532) |
3.3.3.3.6 (632) |
3.3.3.3.7 (732) |
3.3.3.3.8 (832) |
See also
- ccw and cw spinning snub dodecahedron
References
- Jayatilake, Udaya (March 2005). "Calculations on face and vertex regular polyhedra". Mathematical Gazette 89 (514): 76–81.
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
External links
- Eric W. Weisstein, Snub dodecahedron (Archimedean solid) at MathWorld.
- Richard Klitzing, 3D convex uniform polyhedra, s3s5s - snid
- Editable printable net of a Snub Dodecahedron with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- The Snub Dodecahedron made with LEGO by Antonio Nicassio (ITALY)
|
||||||||||||||||||||||||||