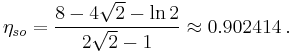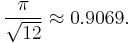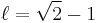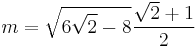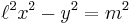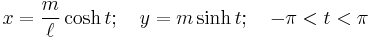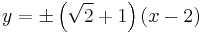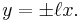Smoothed octagon

The smoothed octagon is a geometrical construction conjectured to have the lowest maximum packing density of the plane of all centrally symmetric convex shapes. It is constructed by replacing the corners of a regular octagon with a section of a hyperbola that is tangent to the two sides adjacent to the corner and asymptotic to the sides adjacent to these.

The smoothed octagon has a maximum packing density, ηso given by

\eta_{so} = \frac{ 8-4\sqrt{2}-\ln{2} }{2\sqrt{2}-1} \approx 0.902414 \, .[1]

This is lower than the maximum packing density of circles, which is

\frac{\pi}{\sqrt{12}} \approx 0.9069.

Contents

Construction

The hyperbola is constructed tangent to two sides of the octagon, and asymptotic to the two adjacent to these. If we define two constants, ℓ and m:

\ell = \sqrt{2} - 1
m = \sqrt{ 6 \sqrt{2} - 8} \frac{\sqrt{2}%2B1}{2}

The hyperbola is then given by the equation

\ell^2x^2-y^2=m^2

or the equivalent parametrisation (for the right-hand branch only):

x=\frac{m}{\ell} \cosh{t}; \quad y = m \sinh t�; \quad -\pi<t<\pi

The lines of the octagon tangent to the hyperbola are

y= \pm \left(\sqrt{2} %2B 1 \right) \left( x-2 \right)

The lines asymptotic to the hyperbola are simply

y = \pm \ell x.

See also

References

  1. ^ Weisstein, Eric W., "Smoothed Octagon" from MathWorld.

External links