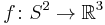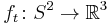Smale's paradox
In differential topology, Smale's paradox states that it is possible to turn a sphere inside out in a three-dimensional space with possible self-intersections but without creating any crease, a process often called sphere eversion (eversion means "to turn inside out"). This is surprising, and is hence deemed a veridical paradox. More precisely, let
be the standard embedding; then there is a regular homotopy of immersions
such that ƒ0 = ƒ and ƒ1 = −ƒ.
Contents |
History
This 'paradox' was discovered by Stephen Smale (1958). It is difficult to visualize a particular example of such a turning, although some digital animations have been produced that make it somewhat easier. The first example was exhibited through the efforts of several mathematicians, including Arnold Shapiro and Bernard Morin who was blind. On the other hand, it is much easier to prove that such a "turning" exists and that is what Smale did.
Smale's graduate adviser Raoul Bott at first told Smale that the result was obviously wrong (Levy 1995). His reasoning was that the degree of the Gauss map must be preserved in such "turning"—in particular it follows that there is no such turning of S1in R2. But the degree of the Gauss map for the embeddings f, −f in R3 are both equal to 1, and do not have opposite sign as one might incorrectly guess. The degree of the Gauss map of all immersions of a 2-sphere in R3 is 1; so there is no obstacle.
See h-principle for further generalizations.
Proof
Smale's original proof was indirect: he identified (regular homotopy) classes of immersions of spheres with a homotopy group of the Stiefel manifold. Since the homotopy group that corresponds to immersions of 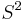 in
in 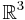 vanishes, the standard embedding and the inside-out one must be regular homotopic. In principle the proof can be unwound to produce an explicit regular homotopy, but this is not easy to do.
vanishes, the standard embedding and the inside-out one must be regular homotopic. In principle the proof can be unwound to produce an explicit regular homotopy, but this is not easy to do.
There are several ways of producing explicit examples and mathematical visualization:
- the method of half-way models: these consist of very special homotopies. This is the original method, first done by Shapiro and Phillips via Boy's surface, later refined by many others. A more recent and definitive refinement (1980s) is minimax eversions, which is a variational method, and consist of special homotopies (they are shortest paths with respect to Willmore energy). The original half-way model homotopies were constructed by hand, and worked topologically but weren't minimal.
- Thurston's corrugations: this is a topological method and generic; it takes a homotopy and perturbs it so that it becomes a regular homotopy.
See also
References
- Francis, George K. (2007), A topological picturebook, Berlin, New York: Springer-Verlag, ISBN 978-0-387-34542-0; 978-0-387-34542-0, MR2265679
- Levy, Silvio (1995), "A brief history of sphere eversions", Making waves, Wellesley, MA: A K Peters Ltd., ISBN 978-1-56881-049-2, MR1357900, http://www.geom.uiuc.edu/docs/outreach/oi/history.html
- Nelson Max, "Turning a Sphere Inside Out", International Film Bureau, Chicago, 1977 (video)
- Anthony Phillips, "Turning a surface inside out, Scientific American, May 1966, pp. 112–120.
- Smale, Stephen (1958), "A classification of immersions of the two-sphere", Transactions of the American Mathematical Society 90: 281–290, ISSN 0002-9947, JSTOR 1993205, MR0104227
External links
- Outside In, full video (short clip here)
- Optiverse video, portions available online
- A History of Sphere Eversions
- "Turning a Sphere Inside Out"
- Software for visualizing sphere eversion