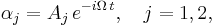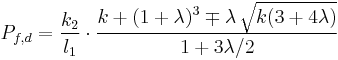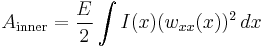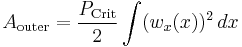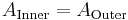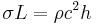Buckling
|
Buckling · Corrosion · Creep · Fatigue · |
In science, buckling is a mathematical instability, leading to a failure mode. Theoretically, buckling is caused by a bifurcation in the solution to the equations of static equilibrium. At a certain stage under an increasing load, further load is able to be sustained in one of two states of equilibrium: an undeformed state or a laterally-deformed state.
In practice, buckling is characterized by a sudden failure of a structural member subjected to high compressive stress, where the actual compressive stress at the point of failure is less than the ultimate compressive stresses that the material is capable of withstanding. For example, during earthquakes, reinforced concrete members may experience lateral deformation of the longitudinal reinforcing bars. This mode of failure is also described as failure due to elastic instability. Mathematical analysis of buckling makes use of an axial load eccentricity that introduces a moment, which does not form part of the primary forces to which the member is subjected. When load is constantly being applied on a member, such as column, it will ultimately become large enough to cause the member to become unstable. Further load will cause significant and somewhat unpredictable deformations, possibly leading to complete loss of load-carrying capacity. The member is said to have buckled, to have deformed.
Columns
The ratio of the effective length of a column to the least radius of gyration of its cross section is called the slenderness ratio (sometimes expressed with the Greek letter lambda, λ). This ratio affords a means of classifying columns. Slenderness ratio is important for design considerations. All the following are approximate values used for convenience.
- A short steel column is one whose slenderness ratio does not exceed 50; an intermediate length steel column has a slenderness ratio ranging from about 50 to 200, and are dominated by the strength limit of the material, while a long steel column may be assumed to have a slenderness ratio greater than 200.
- A short concrete column is one having a ratio of unsupported length to least dimension of the cross section not greater than 10. If the ratio is greater than 10, it is a long column (sometimes referred to as a slender column).
- Timber columns may be classified as short columns if the ratio of the length to least dimension of the cross section is equal to or less than 10. The dividing line between intermediate and long timber columns cannot be readily evaluated. One way of defining the lower limit of long timber columns would be to set it as the smallest value of the ratio of length to least cross sectional area that would just exceed a certain constant K of the material. Since K depends on the modulus of elasticity and the allowable compressive stress parallel to the grain, it can be seen that this arbitrary limit would vary with the species of the timber. The value of K is given in most structural handbooks.
If the load on a column is applied through the center of gravity of its cross section, it is called an axial load. A load at any other point in the cross section is known as an eccentric load. A short column under the action of an axial load will fail by direct compression before it buckles, but a long column loaded in the same manner will fail by buckling (bending), the buckling effect being so large that the effect of the direct load may be neglected. The intermediate-length column will fail by a combination of direct compressive stress and bending.
In 1757, mathematician Leonhard Euler derived a formula that gives the maximum axial load that a long, slender, ideal column can carry without buckling. An ideal column is one that is perfectly straight, homogeneous, and free from initial stress. The maximum load, sometimes called the critical load, causes the column to be in a state of unstable equilibrium; that is, the introduction of the slightest lateral force will cause the column to fail by buckling. The formula derived by Euler for columns with no consideration for lateral forces is given below. However, if lateral forces are taken into consideration the value of critical load remains approximately the same.
where
 = maximum or critical force (vertical load on column),
= maximum or critical force (vertical load on column), = modulus of elasticity,
= modulus of elasticity, = area moment of inertia,
= area moment of inertia, = unsupported length of column,
= unsupported length of column, = column effective length factor, whose value depends on the conditions of end support of the column, as follows.
= column effective length factor, whose value depends on the conditions of end support of the column, as follows.
- For both ends pinned (hinged, free to rotate),
 = 1.0.
= 1.0. - For both ends fixed,
 = 0.50.
= 0.50. - For one end fixed and the other end pinned,
 = 0.699....
= 0.699.... - For one end fixed and the other end free to move laterally,
 = 2.0.
= 2.0.
- For both ends pinned (hinged, free to rotate),
 is the effective length of the column.
is the effective length of the column.
Examination of this formula reveals the following interesting facts with regard to the load-bearing ability of slender columns.
- Elasticity and not compressive strength of the materials of the column determines the critical load.
- The critical load is directly proportional to the second moment of area of the cross section.
- The boundary conditions have a considerable effect on the critical load of slender columns. The boundary conditions determine the mode of bending and the distance between inflection points on the deflected column. The closer together the inflection points are, the higher the resulting capacity of the column.
The strength of a column may therefore be increased by distributing the material so as to increase the moment of inertia. This can be done without increasing the weight of the column by distributing the material as far from the principal axis of the cross section as possible, while keeping the material thick enough to prevent local buckling. This bears out the well-known fact that a tubular section is much more efficient than a solid section for column service.
Another bit of information that may be gleaned from this equation is the effect of length on critical load. For a given size column, doubling the unsupported length quarters the allowable load. The restraint offered by the end connections of a column also affects the critical load. If the connections are perfectly rigid, the critical load will be four times that for a similar column where there is no resistance to rotation (hinged at the ends).
Since the moment of inertia of a surface is its area multiplied by the square of a length called the radius of gyration, the above formula may be rearranged as follows. Using the Euler formula for hinged ends, and substituting A·r2 for I, the following formula results.
where 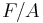 is the allowable stress of the column, and
is the allowable stress of the column, and 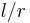 is the slenderness ratio.
is the slenderness ratio.
Since structural columns are commonly of intermediate length, and it is impossible to obtain an ideal column, the Euler formula on its own has little practical application for ordinary design. Issues that cause deviation from the pure Euler strut behaviour include imperfections in geometry in combination with plasticity/non-linear stress strain behaviour of the column's material. Consequently, a number of empirical column formulae have been developed to agree with test data, all of which embody the slenderness ratio. For design, appropriate safety factors are introduced into these formulae. One such formular is the Perry Robertson formula which estimates of the critical buckling load based on an initial (small) curvature. The Rankine Gordon fomular is also based on eperimental results and surgests that a strut will buckle at a load Fmax given by:
where Fe is the euler maximum load and Fc is the maximum compressive load. This formular typically produces a conservative estimate of Fmax.
Self-buckling
A free-standing, vertical column, with density  , Young's modulus
, Young's modulus  , and radius
, and radius  , will buckle under its own weight if its height exceeds a certain critical height:[1][2][3]
, will buckle under its own weight if its height exceeds a certain critical height:[1][2][3]
where g is the acceleration due to gravity, I is the second moment of area of the beam cross section, and B is the first zero of the Bessel function of the first kind of order -1/3, which is equal to 1.86635...
Buckling under tensile dead loading
Usually buckling and instability are associated to compression, but recently Zaccaria, Bigoni, Noselli and Misseroni (2011)[4] have shown that buckling and instability can also occur in elastic structures subject to dead tensile load. An example of a single-degree-of-freedom structure is shown in Fig. 1, where the critical load is also indicated. Another example involving flexure of a structure made up of beam elements governed by the equation of the Euler's elastica is shown in Fig. 2. In both cases, there are no elements subject to compression. The instability and buckling in tension are related to the presence of the slider, the junction between the two rods, allowing only relative sliding between the connected pieces.
Flutter instability
Structures subject to a follower (nonconservative) load may suffer instabilities which are not of the buckling type and therefore are not detectable with a static approach. For instance, the so-called 'Ziegler column' is shown in Fig.3.
This two-degree-of-freedom system does not display a quasi-static buckling, but becomes dynamically unstable. To see this, we note that the equations of motion are
and their linearized version is
Assuming a time-harmonic solution in the form
we find the critical loads for flutter (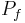 ) and divergence (
) and divergence (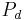 ),
),
where 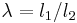 and
and 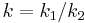 .
.
Flutter instability corresponds to a vibrational motion of increasing amplitude and is shown in Fig.4 (upper part) together with the divergence instability (lower part) consisting in an exponential growth.
Recently, Bigoni and Noselli (2011)[5] have experimentally shown that flutter and divergence instabilities can be directly related to dry friction, watch the movie for more details.
Limit point vs bifurcation buckling
Bifurcation buckling[6][7] is sometimes called Euler buckling even when applied to structures other than Euler columns. As the applied load is increased by a small amount beyond the critical load, the structure deforms into a buckled configuration which is adjacent to the original configuration. For example, the Euler column pictured will start to bow when loaded slightly above its critical load, but will not suddenly collapse.
In structures experiencing limit point instability, if the load is increased infinitesimally beyond the critical load, the structure undergoes a large deformation into a different stable configuration which is not adjacent to the original configuration. An example of this type of buckling is a toggle frame (pictured) which 'snaps' into its buckled configuration.
Bicycle wheels
A conventional bicycle wheel consists of a thin rim kept under high compressive stress by the (roughly normal) inward pull of a large number of spokes. It can be considered as a loaded column that has been bent into a circle. As such, if spoke tension is increased beyond a safe level, the wheel spontaneously fails into a characteristic saddle shape (sometimes called a "taco" or a "pringle") like a three-dimensional Euler column. This is normally a purely elastic deformation and the rim will resume its proper plane shape if spoke tension is reduced slightly.
Surface materials
Buckling is also a failure mode in pavement materials, primarily with concrete, since asphalt is more flexible. Radiant heat from the sun is absorbed in the road surface, causing it to expand, forcing adjacent pieces to push against each other. If the stress is great enough, the pavement can lift up and crack without warning. Going over a buckled section can be very jarring to automobile drivers, described as running over a speed hump at highway speeds.
Similarly, rail tracks also expand when heated, and can fail by buckling, a phenomenon called sun kink. It is more common for rails to move laterally, often pulling the underlain railroad ties (sleepers) along .
Energy method
Often it is very difficult to determine the exact buckling load in complex structures using the Euler formula, due to the difficulty in deciding the constant K. Therefore, maximum buckling load often is approximated using energy conservation. This way of deciding maximum buckling load is often referred to as the energy method in structural analysis.
The first step in this method is to suggest a displacement function. This function must satisfy the most important boundary conditions, such as displacement and rotation. The more accurate the displacement function, the more accurate the result.
In this method, there are two equations used (for small deformations) to approximate the "inner" energy (the potential energy stored in elastic deformation of the structure) and "outer" energy (the work done on the system by external forces).
where 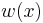 is the displacement function and the subscripts
is the displacement function and the subscripts  and
and 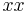 refer to the first and second derivatives of the displacement. Energy conservation yields:
refer to the first and second derivatives of the displacement. Energy conservation yields:
Flexural-torsional buckling
Occurs in compression members only and it can be described as a combination of bending and twisting of a member. And it must be consider for design purposes, since the shape and cross sections are very critical. This mostly occurs in channels, structural tees, double-angle shapes, and equal-leg single angles.
Lateral-torsional buckling
When a simple beam is loaded in flexure, the top side is in compression, and the bottom side is in tension. When a slender member is subjected to an axial force, failure takes place due to bending or torsion rather than direct compression of the material. If the beam is not supported in the lateral direction (i.e., perpendicular to the plane of bending), and the flexural load increases to a critical limit, the beam will fail due to lateral buckling of the compression flange. In wide-flange sections, if the compression flange buckles laterally, the cross section will also twist in torsion, resulting in a failure mode known as lateral-torsional buckling.
Plastic buckling
Buckling will generally occur slightly before the theoretical buckling strength of a structure, due to plasticity of the material. When the compressive load is near buckling, the structure will bow significantly and approach yield. The stress-strain behaviour of materials is not strictly linear even below yield, and the modulus of elasticity decreases as stress increases, with more rapid change near yield. This lower rigidity reduces the buckling strength of the structure and causes premature buckling. This is the opposite effect of the plastic bending in beams, which causes late failure relative to the Euler-Bernoulli beam equation.
Dynamic buckling
If the load on the column is applied suddenly and then released, the column can sustain a load much higher than its static (slowly applied) buckling load. This can happen in a long, unsupported column (rod) used as a drop hammer. The duration of compression at the impact end is the time required for a stress wave to travel up the rod to the other (free) end and back down as a relief wave. Maximum buckling occurs near the impact end at a wavelength much shorter than the length of the rod, at a stress many times the buckling stress if the rod were a statically-loaded column. The critical condition for buckling amplitude to remain less than about 25 times the effective rod straightness imperfection at the buckle wavelength is
where  is the impact stress,
is the impact stress,  is the length of the rod,
is the length of the rod,  is the elastic wave speed, and
is the elastic wave speed, and  is the smaller lateral dimension of a rectangular rod. Because the buckle wavelength depends only on
is the smaller lateral dimension of a rectangular rod. Because the buckle wavelength depends only on  and
and  , this same formula holds for thin cylindrical shells of thickness
, this same formula holds for thin cylindrical shells of thickness  .[8]
.[8]
Buckling of thin cylindrical shells subject to axial loads
Solutions of Donnel's eight order differential equation gives the various buckling modes of a thin cylinder under compression. But this analysis, which is in accordance with the small deflection theory gives much higher values than shown from experiments. So it is customary to find the critical buckling load for various structures which are cylindrical in shape from pre-existing design curves where critical buckling load Fcr is plotted against the ratio R/t, where R is the radius and t is the thickness of the cylinder for various values of L/R, L the length of the cylinder. If cut-outs are present in the cylinder, critical buckling loads as well as pre-buckling modes will be affected. Presence or absence of reinforcements of cut-outs will also affect the buckling load.
Buckling of pipes and pressure vessels subject to external overpressure
Pipes and pressure vessels subject to external overpressure, caused for example by steam cooling down and condensating into water with subsequent massive pressure drop, risk buckling due to compressive hoop stresses. Design rules for calculation of the required wall thickness or reinforcement rings are given in various piping and pressure vessel codes.
See also
References
- ^ Kato, K. (1915). "Mathematical Investigation on the Mechanical Problems of Transmission Line". Journal of the Japan Society of Mechanical Engineers 19: 41.
- ^ Ratzersdorfer, Julius (1936). Die Knickfestigkeit von Stäben und Stabwerken. Wein, Austria: J. Springer. pp. 107–109.
- ^ Cox, Steven J.; C. Maeve McCarthy (1998). "The Shape of the Tallest Column". Society for Industrial and Applied Mathematics 29: 547–554.
- ^ D. Zaccaria, D. Bigoni, G. Noselli and D. Misseroni Structures buckling under tensile dead load. Proceedings of the Royal Society A, 2011, 467, 1686-1700.
- ^ D. Bigoni and G. Noselli, Experimental evidence of flutter and divergence instabilities induced by dry friction. Journal of the Mechanics and Physics of Solids, 2011, 59, 2208–2226.
- ^ "Buckling of Bars, Plates, and Shells" By Robert M. Jones
- ^ "Observations on eigenvalue buckling analysis within a finite element context" by Christopher J. Earls
- ^ Lindberg, H. E., and Florence, A. L., Dynamic Pulse Buckling, Martinus Nijhoff Publishers, 1987, pp. 11–56, 297–298.
- Timoshenko, S. P., and Gere, J. M., Theory of Elastic Stability, 2 ed., McGraw-Hill, 1961.
- Nenezich, M., Thermoplastic Continuum Mechanics, Journal of Aerospace Structures, Vol. 4, 2004.
- The Stability of Elastic Equilibrium by W. T. Koiter, PhD Thesis, 1945.
- Dhakal Rajesh and Koichi Maekawa (October 2002). "Reinforcement Stability and Fracture of Cover Concrete in Reinforced Concrete Members”. [1]
- Willian T. Segui (2007). “Steel Design” Fourth Edition. United States. Chris Carson.
- Analysis and design of flight vehicle structures- E.F.Brune
External links
- The complete theory and example experimental results for long columns are available as a 39-page PDF document at http://lindberglce.com/tech/buklbook.htm
- Video on Buckling under tensile dead loading
- Laboratory for Physical Modeling of Structures and Photoelasticity (University of Trento, Italy)
- http://www.midasuser.com.tw/t_support/tech_pds/files/Tech%20Note-Lateral%20Torsional%20Buckling.pdf
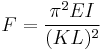
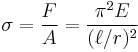
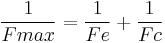
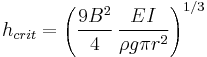
![\
\left\{
\begin{array}{l}
\frac{1}{3} \rho l_1^{2} \left(l_1 %2B 3 l_2\right)\ddot{\alpha}_1 %2B \frac{1}{2} \rho l_1 l_2^{2} \cos(\alpha_1 - \alpha_2)\ddot{\alpha}_2 %2B \frac{1}{2} \rho l_1 l_2^{2} \sin(\alpha_1 - \alpha_2)\dot{\alpha}_2^{2} %2B (k_1 %2B k_2)\alpha_1 - k_2\alpha_2\,%2B \\ [5mm]
%2B (\beta_1 %2B \beta_2)\dot{\alpha}_1 - \beta_2 \dot{\alpha}_2 - l_1 P \sin(\alpha_1 - \alpha_2) = 0 , \\ [5mm]
\frac{1}{2} \rho l_1 l_2^{2} \cos(\alpha_1 - \alpha_2)\ddot{\alpha}_1 %2B \frac{1}{3} \rho l_2^{3}\ddot{\alpha}_2 - \frac{1}{2} \rho l_1 l_2^{2} \sin(\alpha_1 - \alpha_2)\dot{\alpha}_1^{2} - k_2(\alpha_1 - \alpha_2) - \beta_2(\dot{\alpha}_1 - \dot{\alpha}_2) = 0 ,
\end{array}
\right.](/2012-wikipedia_en_all_nopic_01_2012/I/89ee71c790113a39c61ccffebde7db1b.png)
![\
\left\{
\begin{array}{l}
\frac{1}{3} \rho l_1^{2} \left(l_1 %2B 3 l_2\right)\ddot{\alpha}_1 %2B \frac{1}{2} \rho l_1 l_2^{2} \ddot{\alpha}_2 %2B (k_1 %2B k_2)\alpha_1 - k_2\alpha_2 - l_1 P (\alpha_1 - \alpha_2) = 0 , \\ [5mm]
\frac{1}{2} \rho l_1 l_2^{2} \ddot{\alpha}_1 %2B \frac{1}{3} \rho l_2^{3}\ddot{\alpha}_2 - k_2(\alpha_1 - \alpha_2) = 0 .
\end{array}
\right.](/2012-wikipedia_en_all_nopic_01_2012/I/4ff4050fb4d365e2057046cd894cc71f.png)