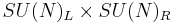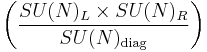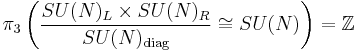Skyrmion
In theoretical physics, a skyrmion is a mathematical model used to model baryons (a subatomic particle). It was conceived by Tony Skyrme.[1]
Overview
A skyrmion is a homotopically non-trivial classical solution of a nonlinear sigma model with a non-trivial target manifold topology—a particular case of a topological soliton. It arises, for example, in chiral models of mesons where the target manifold is a homogeneous space of
(the structure group)
where SU(N)L and SU(N)R are the left and right copies respectively, and SU(N)diag is the diagonal subgroup.
If spacetime has the topology S3×R (for space and time respectively), then classical configurations are classified by an integral winding number because the third homotopy group,
(The congruence sign here refers to homeomorphism, not isomorphism.)
It is possible to add a topological term to the chiral lagrangian whose integral only depends upon the homotopy class. This results in superselection sectors in the quantized model. A toy model for Skyrmion is soliton of Sine-Gordon equation. It can be quantized semi-classically or solved exactly by Bethe Ansatz. After quantization soliton of Sine-Gordon turns into a fermion interacting by means of massive Thirring model.
Other Applications
Besides baryons, it is predicted that Skyrmions could arise in Bose-Einstein Condensates[2], and in superconductors[3]. Skyrmions have also been experimentally observed to describe certain chiral magnetic vortices in thin layers of magnetic materials[4].
References
- ^ Wong, Stephen (2002). "What exactly is a Skyrmion?". arXiv:hep-ph/0202250 [hep/ph].
- ^ Al Khawaja, Usama; Stoof, Henk (2001). "Skyrmions in a ferromagnetic Bose–Einstein condensate". Nature 411 (6840): 918–20. Bibcode 2001Natur.411..918A. doi:10.1038/35082010. PMID 11418849.
- ^ Baskaran (2011). "Possibility of Skyrmion Superconductivity in Doped Antiferromagnet K$_2$Fe$_4$Se$_5$". arXiv:1108.3562 [cond-mat.supr-con].
- ^ Kiselev, N S; Bogdanov, A N; Schäfer, R; Rößler, U K (2011). "Chiral skyrmions in thin magnetic films: New objects for magnetic storage technologies?". Journal of Physics D: Applied Physics 44 (39): 392001. arXiv:1102.2726. Bibcode 2011JPhD...44M2001K. doi:10.1088/0022-3727/44/39/392001.