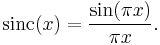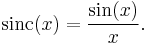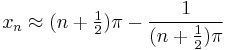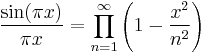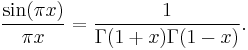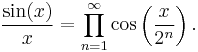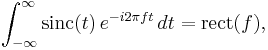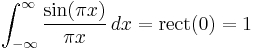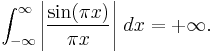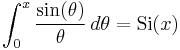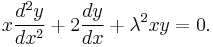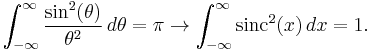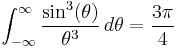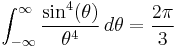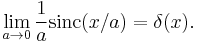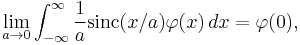Sinc function

In mathematics, the sinc function, denoted by sinc(x) has two nearly equivalent definitions^[1]. In digital signal processing and information theory, the normalized sinc function is commonly defined by

$\mathrm{sinc}(x) = \frac{\sin(\pi x)}{\pi x}.\,\!$

It is qualified as normalized because its integral over all x is 1. All of the zeros of the normalized sinc function are integer values of x. The Fourier transform of the normalized sinc function is the rectangular function with no scaling. This function is fundamental in the concept of reconstructing the original continuous bandlimited signal from uniformly spaced samples of that signal.

In mathematics, the historical unnormalized sinc function is defined by

$\mathrm{sinc}(x) = \frac{\sin(x)}{x}.\,\!$

The only difference between the two definitions is in the scaling of the independent variable (the x-axis) by a factor of π. In both cases, the value of the function at the removable singularity at zero is understood to be the limit value 1. The sinc function is analytic everywhere.

The term "sinc" (English pronunciation: /ˈsɪŋk/) is a contraction of the function's full Latin name, the sinus cardinalis (cardinal sine), first introduced by Phillip M. Woodward in 1953.^[2]^[3]^[4]

1 Properties
2 Relationship to the Dirac delta distribution
3 See also
4 References
5 External links

Properties

The zero crossings of the unnormalized sinc are at nonzero multiples of π, while zero crossings of the normalized sinc occur at nonzero integer values.

The local maxima and minima of the unnormalized sinc correspond to its intersections with the cosine function. That is, sin(ξ)/ξ = cos(ξ) for all points ξ where the derivative of sin(x)/x is zero and thus a local extremum is reached.

A good approximation of the x-coordinate of the n-th extremum with positive x-coordinate is

$x_n \approx (n%2B\tfrac12)\pi - \frac1{(n%2B\frac12)\pi}$

where odd n lead to a local minimum and even n to a local maximum. Besides the extrema at x_n, the curve has an absolute maximum at ξ₀ = (0,1) and because of its symmetry to the y-axis extrema with x-coordinates −x_n.

The normalized sinc function has a simple representation as the infinite product

$\frac{\sin(\pi x)}{\pi x} = \prod_{n=1}^\infty \left(1 - \frac{x^2}{n^2}\right)\,\!$

and is related to the gamma function 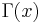$\Gamma(x)$ by Euler's reflection formula:

$\frac{\sin(\pi x)}{\pi x} = \frac{1}{\Gamma(1%2Bx)\Gamma(1-x)}.\,\!$

Euler discovered that

$\frac{\sin(x)}{x} = \prod_{n=1}^\infty \cos\left(\frac{x}{2^n}\right).$

The continuous Fourier transform of the normalized sinc (to ordinary frequency) is rect(f),

$\int_{-\infty}^\infty \mathrm{sinc}(t) \, e^{-i 2 \pi f t}\,dt = \mathrm{rect}(f),\,\!$

where the rectangular function is 1 for argument between −1/2 and 1/2, and zero otherwise. This corresponds to the fact that the sinc filter is the ideal (brick-wall, meaning rectangular frequency response) low-pass filter. This Fourier integral, including the special case

$\int_{-\infty}^\infty \frac{\sin(\pi x)}{\pi x} \, dx = \mathrm{rect}(0) = 1\,\!$

is an improper integral and not a convergent Lebesgue integral, as

$\int_{-\infty}^\infty \left|\frac{\sin(\pi x)}{\pi x} \right|\, dx = %2B\infty.$

The normalized sinc function has properties that make it ideal in relationship to interpolation of sampled bandlimited functions:

It is an interpolating function, i.e., sinc(0) = 1, and sinc(k) = 0 for nonzero integer k.
The functions x_k(t) = sinc(t−k) (k integer) form an orthonormal basis for bandlimited functions in the function space L²(R), with highest angular frequency ω_H = π (that is, highest cycle frequency ƒ_H = 1/2).

Other properties of the two sinc functions include:

The unnormalized sinc is the zero^th order spherical Bessel function of the first kind, 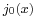$\scriptstyle j_0(x)$ . The normalized sinc is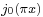 $\scriptstyle j_0(\pi x)$

$\int_0^x \frac{\sin(\theta)}{\theta}\,d\theta = \mathrm{Si}(x) \,\!$

where Si(x) is the sine integral.

λ sinc(λ x) (not normalized) is one of two linearly independent solutions to the linear ordinary differential equation

$x \frac{d^2 y}{d x^2} %2B 2 \frac{d y}{d x} %2B \lambda^2 x y = 0.\,\!$

The other is cos(λ x)/x, which is not bounded at x = 0, unlike its sinc function counterpart.

$\int_{-\infty}^\infty \frac{\sin^2(\theta)}{\theta^2}\,d\theta = \pi \,\! \rightarrow \int_{-\infty}^\infty \mathrm{sinc}^2(x)\,dx = 1.$

where the normalized sinc is meant.

$\int_{-\infty}^\infty \frac{\sin^3(\theta)}{\theta^3}\,d\theta = \frac{3\pi}{4} \,\!$

$\int_{-\infty}^\infty \frac{\sin^4(\theta)}{\theta^4}\,d\theta = \frac{2\pi}{3} \,\!$

Relationship to the Dirac delta distribution

The normalized sinc function can be used as a nascent delta function, meaning that the following weak limit holds:

$\lim_{a\rightarrow 0}\frac{1}{a}\textrm{sinc}(x/a)=\delta(x).$

This is not an ordinary limit, since the left side does not converge. Rather, it means that

$\lim_{a\rightarrow 0}\int_{-\infty}^\infty \frac{1}{a}\textrm{sinc}(x/a)\varphi(x)\,dx = \varphi(0),$

for any smooth function 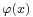$\scriptstyle \varphi(x)$ with compact support.

In the above expression, as a approaches zero, the number of oscillations per unit length of the sinc function approaches infinity. Nevertheless, the expression always oscillates inside an envelope of ±1/(π a x), and approaches zero for any nonzero value of x. This complicates the informal picture of δ(x) as being zero for all x except at the point x = 0 and illustrates the problem of thinking of the delta function as a function rather than as a distribution. A similar situation is found in the Gibbs phenomenon.

References

^ Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., eds. (2010), "Numerical methods", NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248, http://dlmf.nist.gov/3.3
^ Poynton, Charles A. (2003). Digital video and HDTV. Morgan Kaufmann Publishers. p. 147. ISBN 1558607927.
^ Woodward, Phillip M. (1953). Probability and information theory, with applications to radar. London: Pergamon Press. p. 29. ISBN 0890061033. OCLC 488749777. .
^ Also apparently earlier in; Woodward, P. M.; Davies, I. L. (March 1952). "Information theory and inverse probability in telecommunication". Proceedings of the IEE - Part III: Radio and Communication Engineering 99 (58): 37–44. doi:10.1049/pi-3.1952.0011. http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?reload=true&arnumber=5241361.

External links

Weisstein, Eric W., "Sinc Function" from MathWorld.

Sinc function

Contents

Properties

Relationship to the Dirac delta distribution

See also

References

External links