Simson line

In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. The line through these points is the Simson line of P, named for Robert Simson.^[1] The concept was first published, however, by William Wallace.^[2]

The converse is also true; if the three closest points to P on three lines are collinear, and no two of the lines are parallel, then P lies on the circumcircle of the triangle formed by the three lines. The Simson line of a triangle ABC and a point P is just the pedal triangle of ABC and P, in the case when that pedal triangle degenerates to a line.

1 Properties
2 Proof of existence
3 See also
4 References
5 External links

Properties

The Simson line of a vertex of the triangle is the altitude of the triangle dropped from that vertex, and the Simson line of the point diametrically opposite to the vertex is the side of the triangle opposite to that vertex.

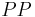If $P$ and $P$ ' are points on the circumcircle, then the angle between the Simson lines of $P$ and $P$ ' is half the angle of the arc $PP$ '. In particular, if the points are diametrically opposite, their Simson lines are perpendicular and in this case the intersection of the lines is on the nine-point circle.

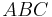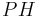Let $H$ denote the orthocenter of the triangle $ABC$ , then the Simson line of $P$ bisects the segment $PH$ in a point that lies on the nine-point circle.

Given two triangles with the same circumcircle, the angle between the Simson lines of a point $P$ on the circumcircle for both triangles doesn't depend of $P$ .

The set of all Simson lines, when drawn, form an envelope in the shape of a deltoid known as the Steiner deltoid of the reference triangle.

The construction of the Simson line that coincides with a side of the reference triangle (see first property above) yields a non trivial point on this side line. This point is the reflection of the foot of the altitude (dropped onto the side line) about the midpoint of the side line being constructed. Furthermore this point is a tangent point between the side of the reference triangle and its Steiner deltoid.

Proof of existence

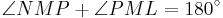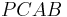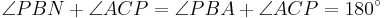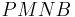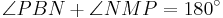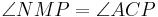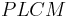The method of proof is to show that $\angle NMP %2B \angle PML = 180^\circ$ . $PCAB$ is a cyclic quadrilateral, so $\angle PBN %2B \angle ACP = \angle PBA %2B \angle ACP = 180^\circ$ . $PMNB$ is a cyclic quadrilateral (Thales' theorem), so $\angle PBN %2B \angle NMP = 180^\circ$ . Hence $\angle NMP = \angle ACP$ . Now $PLCM$ is cyclic, so 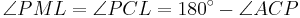$\angle PML = \angle PCL = 180^\circ - \angle ACP$ . 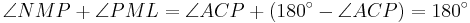Therefore $\angle NMP %2B \angle PML = \angle ACP %2B (180^\circ - \angle ACP) = 180^\circ$ .