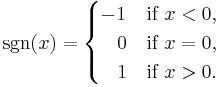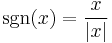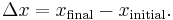Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero. In addition to its application to real numbers, the word sign is used throughout mathematics to indicate aspects of mathematical objects that resemble positivity and negativity, such as the sign of a permutation.
The word sign is also sometimes used to refer to various mathematical symbols, such as the plus and minus symbols and the multiplication symbol. See the table of mathematical symbols for more information on signs and symbols in mathematics.
Contents |
Sign of a number
A real number is said to be positive if it is greater than zero, and negative if it is less than zero. The attribute of being positive or negative is called the sign of the number. Zero itself is not considered to have a sign.
In arithmetic, the sign of a number is often denoted by placing a plus or minus sign before the number. For example, +3 would denote a positive 3, and −3 would denote a negative 3. When no plus or minus sign is given, the default interpretation is that a number is positive.
In algebra, a minus sign is usually thought of as representing the operation of negation, with the negation of a positive number being negative and the negation of a negative number being positive. In this context, it makes sense to write −(−3) = +3.
The sign of any nonzero number can be changed to positive using the absolute value function. For example, the absolute value of −3 and the absolute value of 3 are both equal to 3. In symbols, this would be written |−3| = 3 and |3| = 3.
Sign of zero
The number zero is neither positive nor negative, and therefore has no sign. In arithmetic, +0 and −0 both denote the same number 0, and the negation of zero is zero itself.
In some contexts, such as signed number representations in computing, it makes sense to consider signed versions of zero, with positive zero and negative zero being different numbers (see signed zero).
One also sees +0 and −0 in calculus and mathematical analysis when evaluating certain limits. This notation refers to the behaviour of a function as the input variable approaches 0 from positive or negative values respectively; these behaviours are not necessarily the same.
Terminology for signs
Because zero is neither positive nor negative, the following phrases are sometimes used to refer to the sign of an unknown number:
- A number is positive if it is greater than zero.
- A number is negative if it is less than zero.
- A number is non-negative if it is greater than or equal to zero.
- A number is non-positive if it is less than or equal to zero.
Thus a non-negative number is either positive or zero, while a non-positive number is either negative or zero. For example, the absolute value of a real number is always non-negative, but is not necessarily positive.
The same terminology is sometimes used for functions that take real or integer values. For example, a function would be called positive if all of its values are positive, or non-negative if all of its values are non-negative.
Sign convention
In many contexts the choice of sign convention (which range of values is considered positive and which negative) is natural, whereas in others the choice is arbitrary subject only to consistency, the latter necessitating an explicit sign convention.
Sign function
The sign function or signum function is sometimes used to extract the sign of a number. This function is usually defined as follows:
Thus sgn(x) is 1 when x is positive, and sgn(x) is −1 when x is negative. For nonzero values of x, this function can also be defined by the formula
where |x| is the absolute value of x.
Meanings of sign
Sign of an angle
In many contexts, it is common to associate a sign with the measure of an angle, particularly an oriented angle or an angle of rotation. In such a situation, the sign indicates whether the angle is in the clockwise or counterclockwise direction. Though different conventions can be used, it is common in mathematics to have counterclockwise angles count as positive, and clockwise angles count as negative.
It is also possible to associate a sign to an angle of rotation in three dimensions, assuming the axis of rotation has been oriented. Specifically, a right-handed rotation around an oriented axis typically counts as positive, while a left-handed rotation counts as negative.
Sign of a change
When a quantity x changes over time, the change in the value of x is typically defined by the equation
Using this convention, an increase in x counts as positive change, while a decrease of x counts as negative change. In calculus, this same convention is used in the definition of the derivative. As a result, any increasing function has positive derivative, while a decreasing function has negative derivative.
Sign of a direction
In analytic geometry and physics, it is common to label certain directions as positive or negative. For a basic example, the number line is usually drawn with positive numbers to the right, and negative numbers to the left:
As a result, when discussing linear motion, displacement or velocity to the right is usually thought of as being positive, while similar motion to the left is thought of as being negative.
On the Cartesian plane, the rightward and upward directions are usually thought of as positive, with rightward being the positive x-direction, and upward being the positive y-direction. If a displacement or velocity vector is separated into its vector components, then the horizontal part will be positive for motion to the right and negative for motion to the left, while the vertical part will be positive for motion upward and negative for motion downward.
Signedness in computing
| most-significant bit | |||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | 127 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | 126 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | = | 2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | −1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | −2 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | −127 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | −128 |
In computing, a numeric value may be either signed or unsigned, depending on whether the computer is keeping track of a sign for the number. By restricting a variable to non-negative values only, one more bit can be used for storing the value of a number.
Because of the way arithmetic is done within computers, the sign of a signed variable is usually not stored as a single independent bit, but is instead stored using two's complement or some other signed number representation.
Other meanings
In addition to the sign of a real number, the word sign is also used in various related ways throughout mathematics and the sciences:
- The sign of a permutation is defined to be positive if the permutation is even, and negative if the permutation is odd.
- In graph theory, a signed graph is a graph in which each edge has been marked with a positive or negative sign.
- In mathematical analysis, a signed measure is a generalization of the concept of measure in which the measure of a set may have positive or negative values.
- In a signed-digit representation, each digit of a number may have a positive or negative sign.
- The ideas of signed area and signed volume are sometimes used when it is convenient for certain areas or volumes to count as negative. This is particularly true in the theory of determinants.
- In physics, any electric charge comes with a sign, either positive or negative. By convention, a positive charge is a charge with the same sign as that of a proton, and a negative charge is a charge with the same sign as that of an electron.