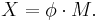Sigma-martingale

In the mathematical theory of probability, sigma-martingale is a semimartingale with an integral representation. Sigma-martingales were introduced by C.S. Chou and M. Emery in 1977 and 1978.^[1] Not every local martingale is a sigma-martingale. In financial mathematics, sigma-martingales appear in the fundamental theorem of asset pricing as an equivalent condition to no free lunch with vanishing risk (a no-arbitrage condition).^[2]

Mathematical definition

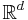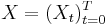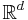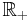An $\mathbb{R}^d$ -valued stochastic process $X = (X_t)_{t = 0}^T$ is a sigma-martingale if it is a semimartingale and there exists an $\mathbb{R}^d$ -valued martingale M and an M-integrable predictable process $\phi$ with values in $\mathbb{R}_%2B$ such that

$X = \phi \cdot M. \,$ ^[1]

^ ^a ^b F. Delbaen; W. Schachermayer (1998). "The Fundamental Theorem of Asset Pricing for Unbounded Stochastic Processes" (pdf). Mathematische Annalen 312: 215–250. http://www.mat.univie.ac.at/~schachermayer/pubs/preprnts/prpr0084.pdf. Retrieved October 14, 2011.
^ Delbaen, Freddy; Schachermayer, Walter. "What is... a Free Lunch?" (pdf). Notices of the AMS 51 (5): 526–528. http://www.ams.org/notices/200405/what-is.pdf. Retrieved October 14, 2011.