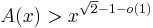Sidon sequence
In number theory, a Sidon sequence (or Sidon set), named after the Hungarian mathematician Simon Sidon, is a sequence A = {a0, a1, a2, ...} of natural numbers in which all pairwise sums ai + aj (i ≤ j) are different. Sidon introduced the concept in his investigations of Fourier series.
The main problem, posed by Sidon[1], is how many elements can A have up to some number x. Despite a large body of research[2] the question remained unsolved for almost 80 years. Recently, it was finally settled[3] by J. Cilleruelo, I. Ruzsa and C. Vinuesa.
Paul Erdős and Pál Turán proved that the number of elements of A up to x is at most ![\sqrt{x}%2BO(\sqrt[4]{x})](/2012-wikipedia_en_all_nopic_01_2012/I/2398aa6f56e34eabca67bec3e98630a4.png) and using a construction of J. Singer they get a
and using a construction of J. Singer they get a 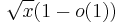 lower bound.
lower bound.
If, however, we consider an infinite Sidon sequence A and let A(x) denote the number of its elements up to x, then Erdos showed that
that is, infinite Sidon sequences are thinner than the above bound for finite sequences.
For the other direction, Chowla and Mian observed that the greedy algorithm gives an infinite Sidon sequence with ![A(x)>c\sqrt[3]{x}](/2012-wikipedia_en_all_nopic_01_2012/I/68c9377b11e56d68c093c0e06bc27279.png) for every x. Ajtai, Komlós, and Szemerédi improved this with a construction[4] of a Sidon sequence with
for every x. Ajtai, Komlós, and Szemerédi improved this with a construction[4] of a Sidon sequence with
The best lower bound to date was given by Imre Z. Ruzsa, who proved[5] that a Sidon sequence with
exists. Erdős conjectured that an infinite Sidon set A exists for which 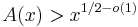 holds. He and Rényi showed[6] the existence of such a sequence a0,a1,...with the weaker property that for every natural number n there are at most c solutions of the equation ai+aj=n for some constant c.
holds. He and Rényi showed[6] the existence of such a sequence a0,a1,...with the weaker property that for every natural number n there are at most c solutions of the equation ai+aj=n for some constant c.
Erdős further conjectured that there exists a nonconstant integer-coefficient polynomial whose values at the natural numbers form a Sidon sequence. Specifically, he asked if the set of fifth powers is a Sidon set. Ruzsa came close to this by showing that there is a real number 0<c<1 such that the range of the function f(x)=x5+[cx4] is a Sidon sequence, where [.] denotes integer part. As c is irrational, f(x) is not a polynomial.
Relationship to Golomb rulers
All finite Sidon sets are Golomb rulers, and vice-versa.
To see this, suppose for a contradiction that S is a Sidon Set and not a Golomb ruler. Since it is not a Golomb ruler, there must be four members such that 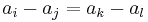 . It follows that
. It follows that 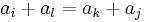 , which contradicts the proposition that S is a Sidon set. Therefore all Sidon Sets must be Golomb rulers. By a similar argument, all Golomb rulers must be Sidon sets.
, which contradicts the proposition that S is a Sidon set. Therefore all Sidon Sets must be Golomb rulers. By a similar argument, all Golomb rulers must be Sidon sets.
See also
References
- ^ Erdős, P.; Turán, P. (1941), "On a problem of Sidon in additive number theory and on some related problems", J. London Math. Soc. 16: 212–215, doi:10.1112/jlms/s1-16.4.212, http://www.renyi.hu/~p_erdos/1941-01.pdf. Addendum, 19 (1944), 208.
- ^ O'Bryant, K. (2004), "A complete annotated bibliography of work related to Sidon sequences", Electronic Journal of Combinatorics 11: 39, http://www.emis.ams.org/journals/EJC/Surveys/ds11.pdf.
- ^ Cilleruelo, J.; Ruzsa, I.; Vinuesa, C. (2010), "Generalized Sidon sets", Advances in Mathematics 225: 2786–2807, http://www.sciencedirect.com/science?_ob=MImg&_imagekey=B6W9F-505G2M9-1-1&_cdi=6681&_user=1675225&_pii=S0001870810001945&_origin=gateway&_coverDate=12%2F01%2F2010&_sk=997749994&view=c&wchp=dGLzVtb-zSkWb&md5=e3adbe497603d81442ebb8f745334fc4&ie=/sdarticle.pdf
- ^ Ajtai, M.; Komlós, J.; Szemerédi, E. (1981), "A dense infinite Sidon sequence", European Journal of Combinatorics 2 (1): 1–11, MR0611925.
- ^ Ruzsa, I. Z. (1998), "An infinite Sidon sequence", Journal of Number Theory 68: 63–71, doi:10.1006/jnth.1997.2192, MR1492889.
- ^ Erdős, P.; Rényi, A. (1960), "Additive properties of random sequences of positive integers", Acta Arithmetica 6: 83–110, MR0120213, http://www.renyi.hu/~p_erdos/1960-02.pdf.
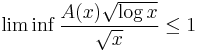
![A(x)>\sqrt[3]{x\log x}.](/2012-wikipedia_en_all_nopic_01_2012/I/a23c6a5225fda86d6ee92099ef1145d0.png)