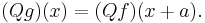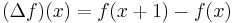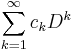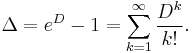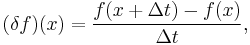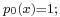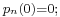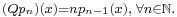Delta operator

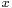In mathematics, a delta operator is a shift-equivariant linear operator $\scriptstyle{ Q:\mathbb K[x] \longrightarrow \mathbb K[x] }$ on the vector space of polynomials in a variable $\scriptstyle x$ over a field 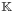$\scriptstyle{ \mathbb K}$ that reduces degrees by one.

To say that 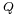$\scriptstyle Q$ is shift-equivariant means that if 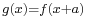$\scriptstyle{ g(x) = f(x %2B a)}$ , then

${ (Qg)(x) = (Qf)(x %2B a)}.\,$

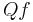In other words, if $f$ is a "shift" of $g$ , then $Qf$ is also a shift of 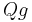$Qg$ , and has the same "shifting vector" $a$ .

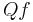To say that an operator reduces degree by one means that if $f$ is a polynomial of degree $n$ , then $Qf$ is either a polynomial of degree 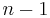$n-1$ , or, in case 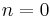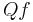$n = 0$ , $Qf$ is 0.

Sometimes a delta operator is defined to be a shift-equivariant linear transformation on polynomials in $x$ that maps $x$ to a nonzero constant. Seemingly weaker than the definition given above, this latter characterization can be shown to be equivalent to the stated definition, since shift-equivariance is a fairly strong condition.

1 Examples
2 Basic polynomials
3 See also
4 References

Examples

The forward difference operator

$(\Delta f)(x) = f(x %2B 1) - f(x)\,$

is a delta operator.

Differentiation with respect to x, written as D, is also a delta operator.

Any operator of the form

$\sum_{k=1}^\infty c_k D^k$

(where Dⁿ(ƒ) = ƒ⁽ⁿ⁾ is the n^th derivative) with 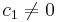$c_1\neq0$ is a delta operator. It can be shown that all delta operators can be written in this form. For example, the difference operator given above can be expanded as

$\Delta=e^D-1=\sum_{k=1}^\infty \frac{D^k}{k!}.$

The generalized derivative of time scale calculus which unifies the forward difference operator with the derivative of standard calculus is a delta operator.

In computer science and cybernetics, the term "discrete-time delta operator" (δ) is generally taken to mean a difference operator

${(\delta f)(x) = {{ f(x%2B\Delta t) - f(x) } \over {\Delta t} }},$

the Euler approximation of the usual derivative with a discrete sample time 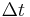$\Delta t$ . The delta-formulation obtains a significant number of numerical advantages compared to the shift-operator at fast sampling.

Basic polynomials

Every delta operator $Q$ has a unique sequence of "basic polynomials", a polynomial sequence defined by three conditions:

$\scriptstyle p_0(x)=1�;$
$\scriptstyle p_{n}(0)=0;$
$\scriptstyle (Qp_n)(x)=np_{n-1}(x), \; \forall n \in \mathbb N.$

Such a sequence of basic polynomials is always of binomial type, and it can be shown that no other sequences of binomial type exist. If the first two conditions above are dropped, then the third condition says this polynomial sequence is a Sheffer sequence -- a more general concept.

References

Nikol'Skii, Nikolai Kapitonovich (1986), Treatise on the shift operator: spectral function theory, Berlin, New York: Springer-Verlag, ISBN 978-0-387-15021-5

Delta operator

Contents

Examples

Basic polynomials

See also

References