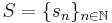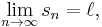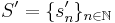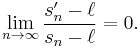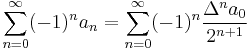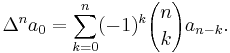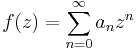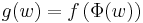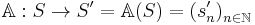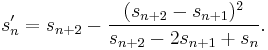Series acceleration
In mathematics, series acceleration is one of a collection of sequence transformations for improving the rate of convergence of a series. Techniques for series acceleration are often applied in numerical analysis, where they are used to improve the speed of numerical integration. Series acceleration techniques may also be used, for example, to obtain a variety of identities on special functions. Thus, the Euler transform applied to the hypergeometric series gives some of the classic, well-known hypergeometric series identities.
Contents |
Definition
Given a sequence
having a limit
an accelerated series is a second sequence
which converges faster to 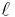 than the original sequence, in the sense that
than the original sequence, in the sense that
If the original sequence is divergent, the sequence transformation acts as an extrapolation method to the antilimit 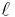 .
.
The mappings from the original to the transformed series may be linear (as defined in the article sequence transformations), or non-linear. In general, the non-linear sequence transformations tend to be more powerful.
Overview
Two classical techniques for series acceleration are Euler's transformation of series[1] and Kummer's transformation of series.[2] A variety of much more rapidly convergent and special-case tools have been developed in the 20th century, including Richardson extrapolation, introduced by Lewis Fry Richardson in the early 20th century but also known and used by Katahiro Takebe in 1722, the Aitken delta-squared process, introduced by Alexander Aitken in 1926 but also known and used by Takakazu Seki in the 18th century, the epsilon algorithm given by Peter Wynn in 1956, the Levin u-transform, and the Wilf-Zeilberger-Ekhad method or WZ method.
For alternating series, several powerful techniques, offering convergence rates from 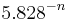 all the way to
all the way to 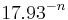 for a summation of
for a summation of  terms, are described by Cohen et al..[3]
terms, are described by Cohen et al..[3]
Euler's transform
A basic example of a linear sequence transformation, offering improved convergence, is Euler's transform. It is intended to be applied to an alternating series; it is given by
where  is the forward difference operator:
is the forward difference operator:
If the original series, on the left hand side, is only slowly converging, the forward differences will tend to become small quite rapidly; the additional power of two further improves the rate at which the right hand side converges.
A particularly efficient numerical implementation of the Euler transform is the van Wijngaarden transformation.[4]
Conformal mappings
A series
- S =
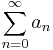
can be written as f(1), where the function f(z) is defined as
The function f(z) can have singularities in the complex plane (branch point singularities, poles or essential singularities), which limit the radius of convergence of the series. If the point z = 1 is close to or on the boundary of the disk of convergence, the series for S will converge very slowly. One can then improve the convergence of the series by means of a conformal mapping that moves the singularities such that the point that is mapped to z = 1, ends up deeper in the new disk of convergence.
The conformal transform 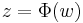 needs to be chosen such that
needs to be chosen such that 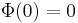 , and one usually chooses a function that has a finite derivative at w = 0. One can assume that
, and one usually chooses a function that has a finite derivative at w = 0. One can assume that 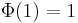 without loss of generality, as one can always rescale w to redefine
without loss of generality, as one can always rescale w to redefine 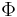 . We then consider the function
. We then consider the function
Since 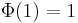 , we have f(1) = g(1). We can obtain the series expansion of g(w) by putting
, we have f(1) = g(1). We can obtain the series expansion of g(w) by putting 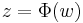 in the series expansion of f(z) because
in the series expansion of f(z) because 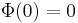 ; the first n terms of the series expansion for f(z) will yield the first n terms of the series expansion for g(w) if
; the first n terms of the series expansion for f(z) will yield the first n terms of the series expansion for g(w) if 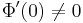 . Putting w = 1 in that series expansion will thus yield a series such that if it converges, it will converge to the same value as the original series.
. Putting w = 1 in that series expansion will thus yield a series such that if it converges, it will converge to the same value as the original series.
Non-linear sequence transformations
Examples of such nonlinear sequence transformations are Padé approximants and Levin-type sequence transformations.
Especially nonlinear sequence transformations often provide powerful numerical methods for the summation of divergent series or asymptotic series that arise for instance in perturbation theory, and may be used as highly effective extrapolation methods.
Aitken method
-
- Main article: Aitken's delta-squared process
A simple nonlinear sequence transformation is the Aitken extrapolation or delta-squared method,
defined by
This transformation is commonly used to improve the rate of convergence of a slowly converging sequence; heuristically, it eliminates the largest part of the absolute error.
See also
References
- ^ Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 3, eqn 3.6.27", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 16, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_16.htm.
- ^ Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 3, eqn 3.6.26", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 16, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_16.htm.
- ^ Henri Cohen, Fernando Rodriguez Villegas, and Don Zagier, "Convergence Acceleration of Alternating Series", Experimental Mathematics, 9:1 (2000) page 3.
- ^ William H. Press, et al., Numerical Recipes in C, (1987) Cambridge University Press, ISBN 0-521-43108-5 (See section 5.1).
- C. Brezinski and M. Redivo Zaglia, Extrapolation Methods. Theory and Practice, North-Holland, 1991.
- G. A. Baker, Jr. and P. Graves-Morris, Padé Approximants, Cambridge U.P., 1996.
- Weisstein, Eric W., "Convergence Improvement" from MathWorld.