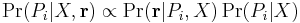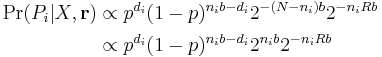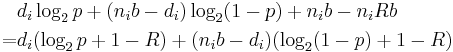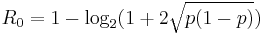Sequential decoding
Sequential decoding is a limited memory technique for decoding tree codes. Sequential decoding is mainly used is as an approximate decoding algorithm for long constraint-length convolutional codes. This approach may not be as accurate as the Viterbi algorithm but can save a substantial amount of computer memory.
Sequential decoding explores the tree code in such a way to try to minimise the computational cost and memory requirements to store the tree.
There is a range of sequential decoding approaches based on choice of metric and algorithm. Metrics include:
- Fano metric
- Zigangirov metric
- Gallager metric
Algorithms include:
- Stack algorithm
- Fano algorithm
- Creeper algorithm
Contents |
Fano metric
Given a partially explored tree (represented by a set of nodes which are limit of exploration), we would like to know the best node from which to explore further. The Fano metric (named after Robert Fano) allows one to calculate from which is the best node to explore further. This metric is optimal given no other constraints (e.g. memory).
For a binary symmetric channel (with error probability  ) the Fano metric can be derived via Bayes theorem. We are interested in following the most likely path
) the Fano metric can be derived via Bayes theorem. We are interested in following the most likely path 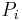 given an explored state of the tree
given an explored state of the tree  and a received sequence
and a received sequence 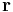 . Using the language of probability and Bayes theorem we want to choose the maximum over
. Using the language of probability and Bayes theorem we want to choose the maximum over  of:
of:
We now introduce the following notation:
 to represent the maximum length of transmission in branches
to represent the maximum length of transmission in branches to represent the number of bits on a branch of the code (the denominator of the code rate,
to represent the number of bits on a branch of the code (the denominator of the code rate,  ).
).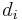 to represent the number of bit errors on path
to represent the number of bit errors on path 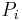 (the Hamming distance between the branch labels and the received sequence)
(the Hamming distance between the branch labels and the received sequence)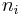 to be the length of
to be the length of 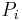 in branches.
in branches.
We express the likelihood 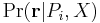 as
as 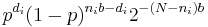 (by using the binary symmetric channel likelihood for the first
(by using the binary symmetric channel likelihood for the first 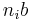 bits followed by a uniform prior over the remaining bits).
bits followed by a uniform prior over the remaining bits).
We express the prior 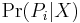 in terms of the number of branch choices one has made,
in terms of the number of branch choices one has made, 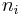 , and the number of branches from each node,
, and the number of branches from each node, 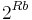 .
.
Therefore:
We can equivalently maximise the log of this probability, i.e.
This last expression is the Fano metric. The important point to see is that we have two terms here: one based on the number of wrong bits and one based on the number of right bits. We can therefore update the Fano metric simply by adding 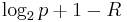 for each non-matching bit and
for each non-matching bit and 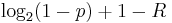 for each matching bit.
for each matching bit.
Computational cutoff rate
For sequential decoding to a good choice of decoding algorithm, the number of states explored wants to remain small (otherwise an algorithm which deliberately explores all states, e.g. the Viterbi algorithm, may be more suitable). For a particular noise level there is a maximum coding rate 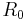 called the computational cutoff rate where there is a finite backtracking limit. For the binary symmetric channel:
called the computational cutoff rate where there is a finite backtracking limit. For the binary symmetric channel:
Algorithms
Stack algorithm
The simplest algorithm to describe is the "stack algorithm" in which the best  paths found so far are stored. Sequential decoding may introduce an additional error above Viterbi decoding when the correct path has
paths found so far are stored. Sequential decoding may introduce an additional error above Viterbi decoding when the correct path has  or more highly scoring paths above it; at this point the best path will drop off the stack and be no longer considered.
or more highly scoring paths above it; at this point the best path will drop off the stack and be no longer considered.
Fano algorithm
The famous Fano algorithm (named after Robert Fano) has a very low memory requirement and hence is suited to hardware implementations. This algorithm explores backwards and forward from a single point on the tree.
References
- John Wozencraft and B. Reiffen, Sequential decoding, ISBN 0262230062
- Rolf Johannsesson and Kamil Sh. Zigangirov, Fundamentals of convolutional coding (chapter 6), ISBN 0470276835
External links
- "Correction trees" - simulator of correction process using priority queue to choose maximum metric node (called weight)