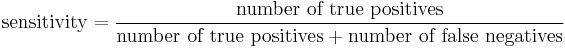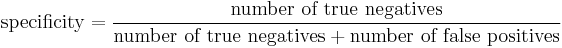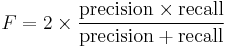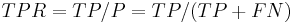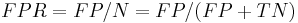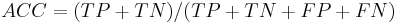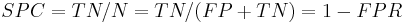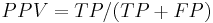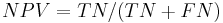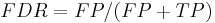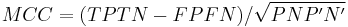Sensitivity and specificity

Sensitivity and specificity are statistical measures of the performance of a binary classification test, also known in statistics as classification function. Sensitivity (also called recall rate in some fields) measures the proportion of actual positives which are correctly identified as such (e.g. the percentage of sick people who are correctly identified as having the condition). Specificity measures the proportion of negatives which are correctly identified (e.g. the percentage of healthy people who are correctly identified as not having the condition). These two measures are closely related to the concepts of type I and type II errors. A theoretical, optimal prediction aims to achieve 100% sensitivity (i.e. predict all people from the sick group as sick) and 100% specificity (i.e. not predict anyone from the healthy group as sick), however theoretically any predictor will possess a minimum error bound known as the Bayes error rate.

For any test, there is usually a trade-off between the measures. For example: in an airport security setting in which one is testing for potential threats to safety, scanners may be set to trigger on low-risk items like belt buckles and keys (low specificity), in order to reduce the risk of missing objects that do pose a threat to the aircraft and those aboard (high sensitivity). This trade-off can be represented graphically as an Receiver operating characteristic curve.

1 Definitions
2 Medical examples
3 Worked example
4 Terminology in information retrieval
5 See also
6 Further reading
7 External links
8 References

Definitions

Imagine a study evaluating a new test that screens people for a disease. Each person taking the test either has or does not have the disease. The test outcome can be positive (predicting that the person has the disease) or negative (predicting that the person does not have the disease). The test results for each subject may or may not match the subject's actual status. In that setting:

True positive: Sick people correctly diagnosed as sick
False positive: Healthy people incorrectly identified as sick
True negative: Healthy people correctly identified as healthy
False negative: Sick people incorrectly identified as healthy.

Sensitivity

Sensitivity relates to the test's ability to identify positive results.

Again, consider the example of the medical test used to identify a disease. The sensitivity of a test is the proportion of people who have the disease who test positive for it. This can also be written as:

$\text{sensitivity} = \frac{\text{number of true positives}}{\text{number of true positives} %2B \text{number of false negatives}}$

If a test has high sensitivity then a negative result would suggest the absence of disease.^[1] For example, a sensitivity of 100% means that the test recognizes all actual positives – i.e. all sick people are recognized as being ill. Thus, in contrast to a high specificity test, negative results in a high sensitivity test are used to rule out the disease.^[1]

From a theoretical point of view, a 'bogus' test kit which always indicates positive, regardless of the disease status of the patient, will achieve 100% sensitivity. Therefore the sensitivity alone cannot be used to determine whether a test is useful in practice.

Sensitivity is not the same as the precision or positive predictive value (ratio of true positives to combined true and false positives), which is as much a statement about the proportion of actual positives in the population being tested as it is about the test.

The calculation of sensitivity does not take into account indeterminate test results. If a test cannot be repeated, the options are to exclude indeterminate samples from analysis (but the number of exclusions should be stated when quoting sensitivity), or, alternatively, indeterminate samples can be treated as false negatives (which gives the worst-case value for sensitivity and may therefore underestimate it).

A test with a high sensitivity has a low type II error rate.

Specificity

Specificity relates to the ability of the test to identify negative results.

Consider the example of the medical test used to identify a disease. The specificity of a test is defined as the proportion of patients who do not have the disease who will test negative for it. This can also be written as:

$\text{specificity} = \frac{\text{number of true negatives}}{\text{number of true negatives} %2B \text{number of false positives}}$

If a test has high specificity, a positive result from the test means a high probability of the presence of disease.^[1]

From a theoretical point of view, a 'bogus' test kit which always indicates negative, regardless of the disease status of the patient, will achieve 100% specificity. Therefore the specificity alone cannot be used to determine whether a test is useful in practice.

A test with a high specificity has a low type I error rate.

Graphical illustration

Medical examples

In medical diagnostics, test sensitivity is the ability of a test to correctly identify those with the disease (true +ve rate), whereas test specificity is the ability of the test to correctly identify those without the disease (true -ve rate).^[2]

If 100 patients known to have a disease were tested, and 43 test positive, then the test has 43% sensitivity. If 100 with no disease are tested and 96 return a negative result, then the test has 96% specificity.

A highly specific test is unlikely to give a false positive result: a positive result should thus be regarded as a true positive. A sign or symptom with very high specificity is often termed pathognomonic. An example of such a test is the inspection for erythema chronicum migrans to diagnose lyme disease.^[3] In contrast, a sensitive test rarely misses a condition, so a negative result should be reassuring (the disease tested for is absent). A sign or symptom with very high sensitivity is often termed sine qua non. An example of such test is a genetic test to find an underlying mutation in certain types of hereditary colon cancer.^[4]^[5]

SPIN and SNOUT are commonly used mnemonics which says: A highly SPecific test, when Positive, rules IN disease (SP-P-IN), and a highly 'SeNsitive' test, when Negative rules OUT disease (SN-N-OUT).

Worked example

Relationships among terms

		Condition (as determined by "Gold standard")
		Condition Positive	Condition Negative
Test Outcome	Test Outcome Positive	True Positive	False Positive (Type I error)	Positive predictive value = Σ True Positive Σ Test Outcome Positive
Test Outcome	Test Outcome Negative	False Negative (Type II error)	True Negative	Negative predictive value = Σ True Negative Σ Test Outcome Negative
		Sensitivity = Σ True Positive Σ Condition Positive	Specificity = Σ True Negative Σ Condition Negative

A worked example: The fecal occult blood (FOB) screen test was used in 2030 people to look for bowel cancer:

		Patients with bowel cancer (as confirmed on endoscopy)
		Condition Positive	Condition Negative
Fecal Occult Blood Screen Test Outcome	Test Outcome Positive	True Positive (TP) = 20	False Positive (FP) = 180	Positive predictive value = TP / (TP + FP) = 20 / (20 + 180) = 10%
Fecal Occult Blood Screen Test Outcome	Test Outcome Negative	False Negative (FN) = 10	True Negative (TN) = 1820	Negative predictive value = TN / (FN + TN) = 1820 / (10 + 1820) ≈ 99.5%
		Sensitivity = TP / (TP + FN) = 20 / (20 + 10) ≈ 67%	Specificity = TN / (FP + TN) = 1820 / (180 + 1820) = 91%

Related calculations

False positive rate (α) = type I error = 1 − specificity = FP / (FP + TN) = 180 / (180 + 1820) = 9%
False negative rate (β) = type II error = 1 − sensitivity = FN / (TP + FN) = 10 / (20 + 10) = 33%
Power = sensitivity = 1 − β
Likelihood ratio positive = sensitivity / (1 − specificity) = 66.67% / (1 − 91%) = 7.4
Likelihood ratio negative = (1 − sensitivity) / specificity = (1 − 66.67%) / 91% = 0.37

Hence with large numbers of false positives and few false negatives, a positive FOB screen test is in itself poor at confirming cancer (PPV = 10%) and further investigations must be undertaken; it did, however, correctly identify 66.7% of all cancers (the sensitivity). However as a screening test, a negative result is very good at reassuring that a patient does not have cancer (NPV = 99.5%) and at this initial screen correctly identifies 91% of those who do not have cancer (the specificity).

Terminology in information retrieval

In information retrieval positive predictive value is called precision, and sensitivity is called recall.

The F-measure can be used as a single measure of performance of the test. The F-measure is the harmonic mean of precision and recall:

$F = 2 \times \frac{\text{precision} \times \text{recall}}{\text{precision} %2B \text{recall}}$

In the traditional language of statistical hypothesis testing, the sensitivity of a test is called the statistical power of the test, although the word power in that context has a more general usage that is not applicable in the present context. A sensitive test will have fewer Type II errors.

Terminology and derivations
from a confusion matrix
true positive (TP) eqv. with hit true negative (TN) eqv. with correct rejection false positive (FP) eqv. with false alarm, Type I error false negative (FN) eqv. with miss, Type II error sensitivity or true positive rate (TPR) eqv. with hit rate, recall $TPR = TP / P = TP / (TP%2BFN)$ false positive rate (FPR) eqv. with false alarm rate, fall-out $FPR = FP / N = FP / (FP %2B TN)$ accuracy (ACC) $ACC = (TP %2B TN) / (TP %2B TN %2B FP %2B FN)$ specificity (SPC) or True Negative Rate $SPC = TN / N = TN / (FP %2B TN) = 1 - FPR$ positive predictive value (PPV) eqv. with precision $PPV = TP / (TP %2B FP)$ negative predictive value (NPV) $NPV = TN / (TN %2B FN)$ false discovery rate (FDR) $FDR = FP / (FP %2B TP)$ Matthews correlation coefficient (MCC) $MCC = (TPTN - FPFN)/ \sqrt{P N P' N'}$ Source: Fawcett (2004).

External links

Calculators:
- Vassar College's Sensitivity/Specificity Calculator

References

^ ^a ^b ^c http://www.cebm.net/index.aspx?o=1042
^ MedStats.Org
^ Ogden NH, Lindsay LR, Morshed M, Sockett PN, Artsob H (January 2008). "The rising challenge of Lyme borreliosis in Canada". Can. Commun. Dis. Rep. 34 (1): 1–19. PMID 18290267. http://www.phac-aspc.gc.ca/publicat/ccdr-rmtc/08vol34/dr-rm3401a-eng.php.
^ Lynch, H. T.; Lynch, J. F.; Lynch, P. M.; Attard, T. (2007). "Hereditary colorectal cancer syndromes: Molecular genetics, genetic counseling, diagnosis and management". Familial Cancer 7 (1): 27–39. doi:10.1007/s10689-007-9165-5. PMID 17999161. edit
^ Lynch, H. T.; Lanspa, S. J. (2010). "Colorectal Cancer Survival Advantage in MUTYH-Associated Polyposis and Lynch Syndrome Families". JNCI Journal of the National Cancer Institute 102 (22): 1687. doi:10.1093/jnci/djq439. edit

Biomedical research: Clinical study design / Design of experiments

Overview	Clinical trial · Clinical trial protocol · Clinical trial management · Academic clinical trials

Controlled study (EBM I to II-1; A to B)	Randomized controlled trial (Blind experiment, Open-label trial)

Observational study (EBM II-2 to II-3; B to C)	Cross-sectional study vs. Longitudinal study, Ecological study Cohort study (Retrospective cohort study, Prospective cohort study) Case-control study (Nested case-control study) Case series · Case study / Case report

Epidemiology/ methods	occurrence: Incidence (Cumulative incidence) · Prevalence (Point prevalence, Period prevalence) association: absolute (Absolute risk reduction, Attributable risk, Attributable risk percent) · relative (Relative risk, Odds ratio, Hazard ratio) other: Virulence · Infectivity · Mortality rate · Morbidity · Case fatality · Specificity and sensitivity · Likelihood-ratios · Pre/post-test probability

Trial/test types	In vitro / In vivo · Animal testing · Animal testing on non-human primates · First-in-man study · Multicenter trial · Seeding trial · Vaccine trial

Analysis of clinical trials	Risk–benefit analysis

Interpretation of results	Selection bias · Correlation does not imply causation · Null result

Category · Glossary · List of topics