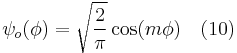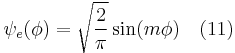Semicircular potential well
In quantum mechanics, the case of a particle in a one-dimensional ring is similar to the particle in a box. The particle follows the path of a semicircle from  to
to  where it cannot escape, because the potential from
where it cannot escape, because the potential from  to
to 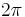 is infinite. Instead there is total reflection, meaning the particle bounces back and forth between
is infinite. Instead there is total reflection, meaning the particle bounces back and forth between  to
to  . The Schrödinger equation for a free particle which is restricted to a semicircle (technically, whose configuration space is the circle
. The Schrödinger equation for a free particle which is restricted to a semicircle (technically, whose configuration space is the circle 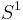 ) is
) is
Contents |
Wave function
Using cylindrical coordinates on the 1 dimensional semicircle, the wave function depends only on the angular coordinate, and so
Substituting the Laplacian in cylindrical coordinates, the wave function is therefore expressed as
The moment of inertia for a semicircle, best expressed in cylindrical coordinates, is 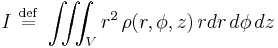 . Solving the integral, one finds that the moment of inertia of a semicircle is
. Solving the integral, one finds that the moment of inertia of a semicircle is 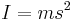 , exactly the same for a hoop of the same radius. The wave function can now be expressed as
, exactly the same for a hoop of the same radius. The wave function can now be expressed as 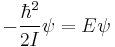 , which is easily solvable.
, which is easily solvable.
Since the particle cannot escape the region from  to
to  , the general solution to this differential equation is
, the general solution to this differential equation is
Defining 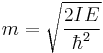 , we can calculate the energy as
, we can calculate the energy as 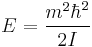 . We then apply the boundary conditions, where
. We then apply the boundary conditions, where  and
and 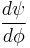 are continuous and the wave function is normalizable:
are continuous and the wave function is normalizable:
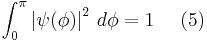 .
.
Like the infinite square well, the first boundary condition demands that the wave function equals 0 at both 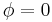 and
and 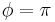 . Basically
. Basically
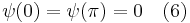 .
.
Since the wave function 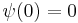 , the coefficient A must equal 0 because
, the coefficient A must equal 0 because 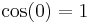 . The wave function also equals 0 at
. The wave function also equals 0 at 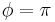 so we must apply this boundary condition. Discarding the trivial solution where B=0, the wave function
so we must apply this boundary condition. Discarding the trivial solution where B=0, the wave function 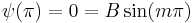 only when m is an integer since
only when m is an integer since 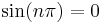 . This boundary condition quantizes the energy where the energy equals
. This boundary condition quantizes the energy where the energy equals 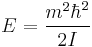 where m is any integer. The condition m=0 is ruled out because
where m is any integer. The condition m=0 is ruled out because 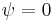 everywhere, meaning that the particle is not in the potential at all. Negative integers are also ruled out.
everywhere, meaning that the particle is not in the potential at all. Negative integers are also ruled out.
We then normalize the wave function, yielding a result where 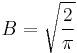 . The normalized wave function is
. The normalized wave function is
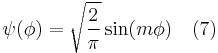 .
.
The ground state energy of the system is 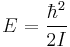 . Like the particle in a box, there exists nodes in the excited states of the system where both
. Like the particle in a box, there exists nodes in the excited states of the system where both 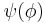 and
and 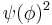 are both 0, which means that the probability of finding the particle at these nodes are 0.
are both 0, which means that the probability of finding the particle at these nodes are 0.
Analysis
Since the wave function is only dependent on the azimuthal angle  , the measurable quantities of the system are the angular position and angular momentum, expressed with the operators
, the measurable quantities of the system are the angular position and angular momentum, expressed with the operators  and
and 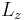 respectively.
respectively.
Using cylindrical coordinates, the operators  and
and 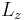 are expressed as
are expressed as  and
and 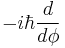 respectively, where these observables play a role similar to position and momentum for the particle in a box. The commutation and uncertainty relations for angular position and angular momentum are given as follows:
respectively, where these observables play a role similar to position and momentum for the particle in a box. The commutation and uncertainty relations for angular position and angular momentum are given as follows:
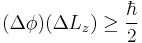 where
where 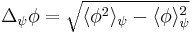 and
and 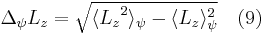
Boundary conditions
As with all quantum mechanics problems, if the boundary conditions are changed so does the wave function. If a particle is confined to the motion of an entire ring ranging from 0 to 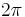 , the particle is subject only to a periodic boundary condition (see particle in a ring). If a particle is confined to the motion of
, the particle is subject only to a periodic boundary condition (see particle in a ring). If a particle is confined to the motion of 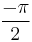 to
to 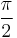 , the issue of even and odd parity becomes important.
, the issue of even and odd parity becomes important.
The wave equation for such a potential is given as:
where 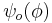 and
and 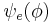 are for odd and even m respectively.
are for odd and even m respectively.
Similarly, if the semicircular potential well is a finite well, the solution will resemble that of the finite potential well where the angular operators  and
and 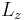 replace the linear operators x and p.
replace the linear operators x and p.
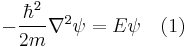
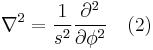
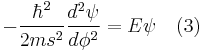
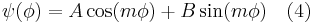
![[\phi, L_z] = i \hbar \ \psi(\phi) \quad (8)](/2012-wikipedia_en_all_nopic_01_2012/I/6e776dafedc6d7105110e13a2e1933d2.png)