Semi-s-cobordism

In mathematics, a cobordism (W, M, M−) of an (n + 1)-dimensionsal manifold (with boundary) W between its boundary components, two n-manifolds M and M− (n.b.: the original creator of this topic, Jean-Claude Hausmann, used the notation M− for the right-hand boundary of the cobordism), is called a semi-s-cobordism if (and only if) the inclusion 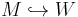M \hookrightarrow W is a simple homotopy equivalence (as in an s-cobordism) but the inclusion 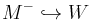M^- \hookrightarrow W is not a homotopy equivalence at all.

A consequence of (W, M, M−) being a semi-s-cobordism is that the kernel of the derived homomorphism on fundamental groups 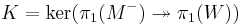K = \ker(\pi_1(M^{-}) \twoheadrightarrow \pi_1(W)) is perfect. A corollary of this is that 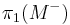\pi_1(M^{-}) solves the group extension problem 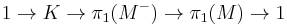1 \rightarrow K \rightarrow \pi_1(M^{-}) \rightarrow \pi_1(M) \rightarrow 1. The solutions to the group extension problem for proscribed quotient group 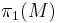\pi_1(M) and kernel group K are classified up to congruence (see Homology by MacLane, e.g.), so there are restrictions on which n-manifolds can be the right-hand boundary of a semi-s-cobordism with proscribed left-hand boundary M and superperfect kernel group K.

Note that if (W, M, M−) is a semi-s-cobordism, then (W, M−, M) is a Plus cobordism. (This justifies the use of M− for the right-hand boundary of a semi-s-cobordism, a play on the traditional use of M+ for the right-hand boundary of a Plus cobordism.) Thus, a semi-s-cobordism may be thought of as an inverse to Quillen's Plus construction in the manifold category. Note that (M−)+ must be diffeomorphic (respectively, piecewise-linearly (PL) homeomorphic) to M but there may be a variety of choices for (M+)− for a given closed smooth (respectively, PL) manifold M.

References