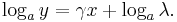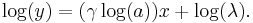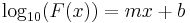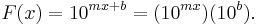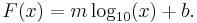Semi-log plot

In science and engineering, a semi-log graph or semi-log plot is a way of visualizing data that are changing with an exponential relationship. One axis is plotted on a logarithmic scale. This kind of plot is useful when one of the variables being plotted covers a large range of values and the other has only a restricted range – the advantage being that it can bring out features in the data that would not easily be seen if both variables had been plotted linearly.^[1]

All functions of the form 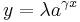$y=\lambda a^{\gamma x}$ form straight lines, since taking logs of both sides is equal to

$\log_a y = \gamma x %2B \log_a \lambda.$

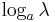This can easily be seen as a line in slope-intercept form with $\gamma$ as slope, $\log_a \lambda$ as the y-intercept. To facilitate use with logarithmic tables, one usually takes logs to base 10 or e:

$\log (y) = (\gamma \log (a)) x %2B \log (\lambda).$

The term log-lin is used to describe a semi-log plot with a logarithmic scale on the y-axis, and a linear scale on the x-axis. Likewise, a lin-log graph uses a logarithmic scale on the x-axis, and a linear scale on the y-axis.

A log-log graph uses the logarithmic scale for both axes, and hence is not a semi-log graph.

On a semi-log graph the spacing of the scale on the y-axis is proportional to the logarithm of the number, not the number itself. It is equivalent to converting the Y values to their log, and plotting the data on lin-lin scales.

1 Equations
2 Real-world examples
3 See also
4 References

Equations

The equation for a line with an ordinate axis logarithmically scaled would be:

$\log_{10}(F(x)) = mx %2B b$

$F(x) = 10^{mx %2B b} = (10^{mx})(10^b).$

The equation of a line on a plot where the abscissa axis is scaled logarithmically would be

$F(x) = m \log_{10}(x) %2B b. \,$

Real-world examples

Phase diagram of water

In physics and chemistry, a plot of logarithm of pressure against temperature can be used to illustrate the various phases of a substance, as in the following for water:

2009 "swine flu" progression

While ten is the most common base, there are times when other bases are more appropriate, as in this example:

Microbial growth

In biology and biological engineering, the change in numbers of microbes due to asexual reproduction and nutrient exhaustion is commonly illustrated by a semi-log plot. Time is usually the independent axis, with the logarithm of the number or mass of bacteria or other microbe as the dependent variable. This forms a plot with four distinct phases, as shown below.

References

^ M. Bourne Graphs on Logarithmic and Semi-Logarithmic Paper (www.intmath.com)