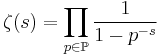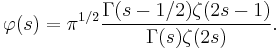Selberg zeta function

The Selberg zeta-function was introduced by Atle Selberg (1956). It is analogous to the famous Riemann zeta function

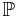\zeta(s) = \prod_{p\in\mathbb{P}} \frac{1}{1-p^{-s}}

where \mathbb{P} is the set of prime numbers. The Selberg zeta-function uses the lengths of simple closed geodesics instead of the primes numbers.

For any hyperbolic surface of finite area there is an associated Selberg zeta-function; this function is a meromorphic function defined in the complex plane. The zeta function is defined in terms of the closed geodesics of the surface.

The zeros and poles of the Selberg zeta-function, Z(s), can be described in terms of spectral data of the surface.

The zeros are at the following points:

  1. For every cusp form with eigenvalue 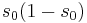s_0(1-s_0) there exists a zero at the point 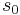s_0. The order of the zero equals the dimension of the corresponding eigenspace. (A cusp form is an eigenfunction to the Laplace-Beltrami operator which has Fourier expansion with zero constant term.)
  2. The zeta-function also has a zero at every pole of the determinant of the scattering matrix, 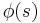\phi(s) . The order of the zero equals the order of the corresponding pole of the scattering matrix.

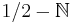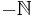The zeta-function also has poles at 1/2 - \mathbb{N} , and can have zeros or poles at the points - \mathbb{N} .

Selberg zeta-function for the modular group

For the case where the surface is 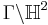\Gamma \backslash \mathbb{H}^2 , where 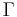\Gamma is the modular group, the Selberg zeta-function is of special interest. For this special case the Selberg zeta-function is intimately connected to the Riemann zeta-function.

In this case the scattering matrix is given by:

\varphi(s) = \pi^{1/2} \frac{ \Gamma(s-1/2) \zeta(2s-1) }{ \Gamma(s) \zeta(2s) }.

In particular, we see that if the Riemann zeta-function has a zero at 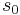s_0, then the scattering matrix has a pole at 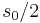s_0/2, and hence the Selberg zeta-function has a zero at s_0/2.

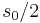References