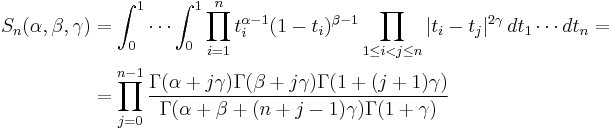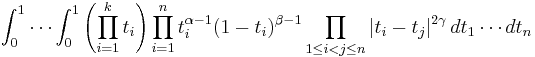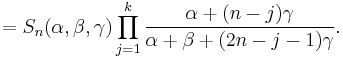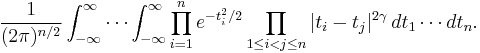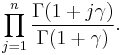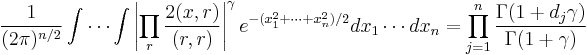Selberg integral
In mathematics the Selberg integral is a generalization of Euler beta function to n dimensions introduced and proven by Atle Selberg (1944).
Contents |
Selberg's integral formula
Selberg's formula implies Dixon's identity for well poised hypergeometric series, and some special cases of Dyson's conjecture.
Aomoto's integral formula
Aomoto (1987) proved a slightly more general integral formula:
Mehta's integral
Mehta's integral is
It is the partition function for a gas of point charges moving on a line that are attracted to the origin (Mehta 2004). Its value can be deduced from that of the Selberg integral, and is
This was conjectured by Mehta & Dyson (1963), who were unaware of Selberg's earlier work.
Macdonald's integral
Macdonald (1982) conjectured the following extension of Mehta's integral to all finite root systems, Mehta's original case corresponding to the An−1 root system.
The product is over the roots r of the roots system and the numbers dj are the degrees of the generators of the ring of invariants of the reflection group. Opdam (1989) gave a uniform proof for all crystallographic reflection groups. Several years later he proved it in full generality (Opdam (1993)), making use of computer-aided calculations by Garvan.
References
- Andrews, George E.; Askey, Richard; Roy, Ranjan (1999), Special functions, Encyclopedia of Mathematics and its Applications, 71, Cambridge University Press, ISBN 978-0-521-62321-6; 978-0-521-78988-2, MR1688958 (Chapter 8)
- Aomoto, K (1987), "On the complex Selberg integral", The Quarterly Journal of Mathematics 38 (4): 385–399, doi:10.1093/qmath/38.4.385
- Forrester, Peter J.; Warnaar, S. Ole (2008), "The importance of the Selberg integral", Bull. Amer. Math. Soc. 45 (4): 489–534, doi:10.1090/S0273-0979-08-01221-4, http://www.ams.org/bull/2008-45-04/S0273-0979-08-01221-4/home.html
- Macdonald, I. G. (1982), "Some conjectures for root systems", SIAM Journal on Mathematical Analysis 13 (6): 988–1007, doi:10.1137/0513070, ISSN 0036-1410, MR674768
- Mehta, Madan Lal (2004), Random matrices, Pure and Applied Mathematics (Amsterdam), 142 (3rd ed.), Elsevier/Academic Press, Amsterdam, ISBN 978-0-12-088409-4, MR2129906
- Mehta, Madan Lal; Dyson, Freeman J. (1963), "Statistical theory of the energy levels of complex systems. V", Journal of Mathematical Physics 4 (5): 713–719, doi:10.1063/1.1704009, ISSN 0022-2488, MR0151232
- Opdam, E.M. (1989), "Some applications of hypergeometric shift operators", Invent. Math. 98 (1): 275–282, doi:10.1007/BF01388841, MR1010152
- Opdam, E.M. (1993), "Dunkl operators, Bessel functions and the discriminant of a finite Coxeter group", Compositio Math. 85 (3): 333–373, MR1214452, Zbl 0778.33009, http://www.numdam.org/item?id=CM_1993__85_3_333_0
- Selberg, Atle (1944), "Remarks on a multiple integral", Norsk Mat. Tidsskr. 26: 71–78, MR0018287