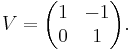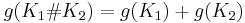Seifert surface

In mathematics, a Seifert surface (named after German mathematician Herbert Seifert^[1]^[2]) is a surface whose boundary is a given knot or link.

Such surfaces can be used to study the properties of the associated knot or link. For example, many knot invariants are most easily calculated using a Seifert surface. Seifert surfaces are also interesting in their own right, and the subject of considerable research.

Specifically, let L be a tame oriented knot or link in Euclidean 3-space (or in the 3-sphere). A Seifert surface is a compact, connected, oriented surface S embedded in 3-space whose boundary is L such that the orientation on L is just the induced orientation from S, and every connected component of S has non-empty boundary.

Note that any compact, connected, oriented surface with nonempty boundary in Euclidean 3-space is the Seifert surface associated to its boundary link. A single knot or link can have many different inequivalent Seifert surfaces. A Seifert surface must be oriented. It is possible to associate unoriented (and not necessarily orientable) surfaces to knots as well.

1 Examples
2 Existence and Seifert matrix
3 Genus of a knot
4 See also
5 References
6 External links

Examples

The standard Möbius strip has the unknot for a boundary but is not considered to be a Seifert surface for the unknot because it is not orientable.

The "checkerboard" coloring of the usual minimal crossing projection of the trefoil knot gives a Mobius strip with three half twists. As with the previous example, this is not a Seifert surface as it is not orientable. Applying Seifert's algorithm to this diagram, as expected, does produce a Seifert surface; in this case, it is a punctured torus of genus g=1, and the Seifert matrix is

$V = \begin{pmatrix}1 & -1 \\ 0 & 1\end{pmatrix}.$

Existence and Seifert matrix

It is a theorem that any link always has an associated Seifert surface. This theorem was first published by Frankl and Pontrjagin in 1930.^[3] A different proof was published in 1934 by Herbert Seifert and relies on what is now called the Seifert algorithm. The algorithm produces a Seifert surface $S$ , given a projection of the knot or link in question.

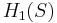Suppose that link has m components (m=1 for a knot), the diagram has d crossing points, and resolving the crossings (preserving the orientation of the knot) yields f circles. Then the surface $S$ is constructed from f disjoint disks by attaching d bands. The homology group $H_1(S)$ is free abelian on 2g generators, where

g = (2 + d − f − m)/2

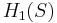is the genus of $S$ . The intersection form Q on $H_1(S)$ is skew-symmetric, and there is a basis of 2g cycles

a₁,a₂,...,a_2g

with

Q=(Q(a_i,a_j))

the direct sum of g copies of

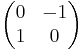$\begin{pmatrix} 0 & -1 \\ 1 & 0\end{pmatrix}$ .

The 2g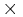 $\times$ 2g integer Seifert matrix

V=(v(i,j)) has

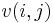$v(i,j)$ the linking number in Euclidean 3-space (or in the 3-sphere) of a_i and the pushoff of a_j out of the surface, with

$V-V$ ^* $=Q$

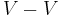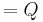
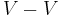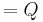where V^*=(v(j,i)) the transpose matrix. Every integer 2g $\times$ 2g matrix $V$ with $V-V$ ^* $=Q$ arises as the Seifert matrix of a knot with genus g Seifert surface.

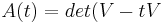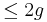The Alexander polynomial is computed from the Seifert matrix by $A(t)=det(V-tV$ ^*), which is a polynomial in the indeterminate $t$ of degree $\leq 2g$ . The Alexander polynomial is independent of the choice of Seifert surface $S$ , and is an invariant of the knot or link.

The signature of a knot is the signature of the symmetric Seifert matrix 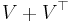$V%2BV^\top$ . It is again an invariant of the knot or link.

Genus of a knot

Seifert surfaces are not at all unique: a Seifert surface S of genus g and Seifert matrix V can be modified by a surgery, to be replaced by a Seifert surface S' of genus g+1 and Seifert matrix

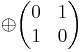V'=V $\oplus \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$ .

The genus of a knot K is the knot invariant defined by the minimal genus g of a Seifert surface for K.

For instance:

An unknot—which is, by definition, the boundary of a disc—has genus zero. Moreover, the unknot is the only knot with genus zero.
The trefoil knot has genus one, as does the figure-eight knot.
The genus of a (p,q)-torus knot is (p − 1)(q − 1)/2
The degree of the Alexander polynomial is a lower bound on twice the genus of the knot.

A fundamental property of the genus is that it is additive with respect to the knot sum:

$g(K_1 \# K_2) = g(K_1) %2B g(K_2)$

References

^ Seifert, H. (1934). "Über das Geschlecht von Knoten". Math. Annalen 110 (1): 571–592. doi:10.1007/BF01448044. (German)
^ van Wijk, Jarke J.; Cohen, Arjeh M. (2006). "Visualization of Seifert Surfaces". IEEE Trans. on Visualization and Computer Graphics 12 (4): 485–496. doi:10.1109/TVCG.2006.83.
^ Frankl, F.; Pontrjagin, L. (1930). "Ein Knotensatz mit Anwendung auf die Dimensionstheorie". Math. Annalen 102 (1): 785–789. doi:10.1007/BF01782377. (German)

External links

The SeifertView programme of Jack van Wijk visualizes the Seifert surfaces of knots constructed using Seifert's algorithm.