Scleronomous

A mechanical system is scleronomous if the equations of constraints do not contain the time as an explicit variable. Such constraints are called scleronomic constraints.

Contents

Application

Main article：Generalized velocity

In 3-D space, a particle with mass 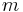m\,\! , velocity 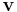\mathbf{v}\,\! has kinetic energy

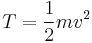T =\frac{1}{2}m v^2 \,\! .

Velocity is the derivative of position with respect time. Use chain rule for several variables:

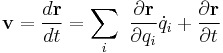\mathbf{v}=\frac{d\mathbf{r}}{dt}=\sum_i\ \frac{\partial \mathbf{r}}{\partial q_i}\dot{q}_i%2B\frac{\partial \mathbf{r}}{\partial t}\,\! .

Therefore,

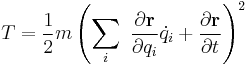T =\frac{1}{2}m \left(\sum_i\ \frac{\partial \mathbf{r}}{\partial q_i}\dot{q}_i%2B\frac{\partial \mathbf{r}}{\partial t}\right)^2\,\! .

Rearranging the terms carefully,[1]

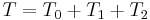T =T_0%2BT_1%2BT_2\,\! :
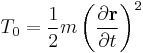T_0=\frac{1}{2}m\left(\frac{\partial \mathbf{r}}{\partial t}\right)^2\,\! ,
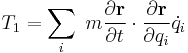T_1=\sum_i\ m\frac{\partial \mathbf{r}}{\partial t}\cdot \frac{\partial \mathbf{r}}{\partial q_i}\dot{q}_i\,\! ,
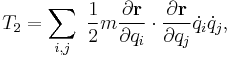T_2=\sum_{i,j}\ \frac{1}{2}m\frac{\partial \mathbf{r}}{\partial q_i}\cdot \frac{\partial \mathbf{r}}{\partial q_j}\dot{q}_i\dot{q}_j,\! .

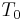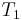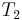T_0\,\! , T_1\,\! , T_2\,\! are respectively homogeneous functions of degree 0, 1, and 2 in generalized velocities. If this system is scleronomous, then, the position does not depend explicitly with time:

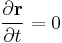\frac{\partial \mathbf{r}}{\partial t}=0\,\! .

Therefore, only term 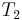T_2\,\! does not vanish:

T =T_2\,\! .

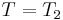Kinetic energy is a homogeneous function of degree 2 in generalized velocities .

Example: pendulum

As shown at right, a simple pendulum is a system composed of a weight and a string. The string is attached at the top end to a pivot and at the bottom end to a weight. Being inextensible, the string’s length is a constant. Therefore, this system is scleronomous; it obeys scleronomic constraint

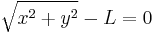\sqrt{x^2%2By^2} - L=0\,\! ,

where 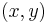(x,y)\,\! is the position of the weight and 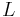L\,\! is length of the string.

Take a more complicated example. Refer to the next figure at right, Assume the top end of the string is attached to a pivot point undergoing a simple harmonic motion

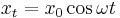x_t=x_0\cos\omega t\,\! ,

where 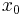x_0\,\! is amplitude, 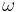\omega\,\! is angular frequency, and 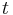t\,\! is time.

Although the top end of the string is not fixed, the length of this inextensible string is still a constant. The distance between the top end and the weight must stay the same. Therefore, this system is a rheonomous; it obeys rheonomic constraint

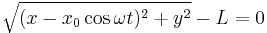\sqrt{(x - x_0\cos\omega t)^2%2By^2} - L=0\,\! .

See also

References

  1. ^ Goldstein, Herbert (1980). Classical Mechanics (3rd ed.). United States of America: Addison Wesley. p. 25. ISBN 0201657023.