Schur's property

In mathematics, Schur's property, named after Issai Schur, is the property of normed spaces that is satisfied precisely if weak convergence of sequences entails convergence in norm.

1 Motivation
2 Definition
3 Name
4 See also
5 Notes
6 References

Motivation

When we are working in a normed space X and we have a sequence 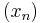$(x_{n})$ that converges weakly to $x$ (see weak convergence), then a natural question arises. Does the sequence converge in perhaps a more desirable manner? That is, does the sequence converge to $x$ in norm?

Definition

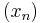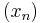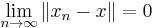Suppose that we have a normed space (X, ||·||), $x$ an arbitrary member of X, and $(x_{n})$ an arbitrary sequence in the space. We say that X has Schur's property if $(x_{n})$ converging weakly to $x$ implies that $\lim_{n\to\infty} \Vert x_n - x\Vert = 0$ . In other words, the weak and strong topologies share the same convergent sequences. Note however that weak and strong topologies are always distinct in infinite-dimensional space.

Name

This property was named after the early 20th century mathematician Issai Schur who showed that ℓ¹ had the above property in his 1921 paper.^[1]

Notes

^ J. Schur, "Über lineare Transformationen in der Theorie der unendlichen Reihen", Journal für die reine und angewandte Mathematik, 151 (1921) pp. 79-111

References

[|Megginson, Robert E.] (1998), An Introduction to Banach Space Theory, New York Berlin Heidelberg: Springer-Verlag, ISBN 0-387-98431-3