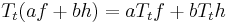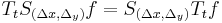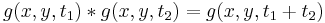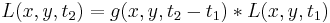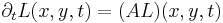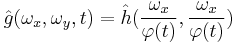Scale-space axioms
In image processing and computer vision, a scale-space framework can be used to represent an image as a family of gradually smoothed images. This framework is very general and a variety of scale-space representations exist. A typical approach for choosing a particular type of scale-space representation is to establish a set of scale-space axioms, describing basic properties of the desired scale-space representation and often chosen so as to make the representation useful in practical applications. Once established, the axioms narrow the possible scale-space representations to a smaller class, typically with only a few free parameters.
A set of standard scale space axioms, discussed below, leads to the linear Gaussian scale-space, which is the most common type of scale space used in image processing and computer vision.
Scale space axioms for the linear scale-space representation
The linear scale-space representation 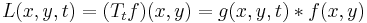 of signal
of signal 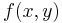 obtained by smoothing with the Gaussian kernel
obtained by smoothing with the Gaussian kernel 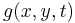 satisfies a number of properties 'scale-space axioms' that make it a special form of multi-scale representation:
satisfies a number of properties 'scale-space axioms' that make it a special form of multi-scale representation:
- linearity
 and
and  are signals while
are signals while  and
and  are constants,
are constants,
- shift invariance'
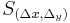 denotes the shift (translation) operator
denotes the shift (translation) operator 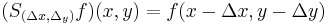
- the semi-group structure
- existence of an infinitesimal generator

- non-creation of local extrema (zero-crossings) in one dimension,
- non-enhancement of local extrema in any number of dimensions
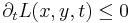 at spatial maxima and
at spatial maxima and 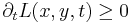 at spatial minima,
at spatial minima,
- rotational symmetry
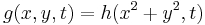 for some function
for some function  ,
,
- scale invariance
 and
and 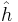 where
where 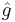 denotes the Fourier transform of
denotes the Fourier transform of  ,
,
- positivity:
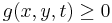 ,
,
- normalization:
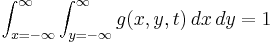 .
.
In fact, it can be shown that the Gaussian kernel is a unique choice given several different combinations of subsets of these scale-space axioms:[1][2][3][4][5][6][7][8][9] most of the axioms (linearity, shift-invariance, semigroup) correspond to scaling being a semigroup of shift-invariant linear operator, which is satisfied by a number of families integral transforms, while "non-creation of local extrema" is the crucial axiom which related scale-spaces to smoothing (formally, parabolic partial differential equations), and hence selects for the Gaussian.
The Gaussian kernel is also separable in Cartesian coordinates, i.e. 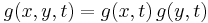 . Separability is, however, not counted as a scale-space axiom, since it is a coordinate dependent property related to issues of implementation. In addition, the requirement of separability in combination with rotational symmetry per se fixates the smoothing kernel to be a Gaussian.
. Separability is, however, not counted as a scale-space axiom, since it is a coordinate dependent property related to issues of implementation. In addition, the requirement of separability in combination with rotational symmetry per se fixates the smoothing kernel to be a Gaussian.
In the computer vision, image processing and signal processing literature there are many other multi-scale approaches, using wavelets and a variety of other kernels, that do not exploit or require the same requirements as scale-space descriptions do; please see the article on related multi-scale approaches. There has also been work on discrete scale-space concepts that carry the scale-space properties over to the discrete domain; see the article on scale-space implementation for examples and references.
See also
References
- ^ Koenderink, Jan "The structure of images", Biological Cybernetics, 50:363–370, 1984
- ^ J. Babaud, A. P. Witkin, M. Baudin, and R. O. Duda, Uniqueness of the Gaussian kernel for scale-space filtering. IEEE Trans. Pattern Anal. Machine Intell. 8(1), 26–33, 1986.
- ^ A. Yuille, T.A. Poggio: Scaling theorems for zero crossings. IEEE Trans. Pattern Analysis & Machine Intelligence, Vol. PAMI-8, no. 1, pp. 15–25, Jan. 1986.
- ^ Lindeberg, T., "Scale-space for discrete signals," PAMI(12), No. 3, March 1990, pp. 234–254.
- ^ Lindeberg, Tony, Scale-Space Theory in Computer Vision, Kluwer, 1994,
- ^ Pauwels, E., van Gool, L., Fiddelaers, P. and Moons, T.: An extended class of scale-invariant and recursive scale space filters, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 17, No. 7, pp. 691–701, 1995.
- ^ Lindeberg, T.: On the axiomatic foundations of linear scale-space: Combining semi-group structure with causailty vs. scale invariance. In: J. Sporring et al. (eds.) Gaussian Scale-Space Theory: Proc. PhD School on Scale-Space Theory , (Copenhagen, Denmark, May 1996), pages 75–98, Kluwer Academic Publishers, 1997.
- ^ Florack, Luc, Image Structure, Kluwer Academic Publishers, 1997.
- ^ Weickert, J. Linear scale space has first been proposed in Japan. Journal of Mathematical Imaging and Vision, 10(3):237–252, 1999.