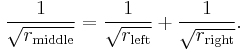Sangaku
Sangaku or San Gaku (算額; lit. mathematical tablet) are Japanese geometrical puzzles in Euclidean geometry on wooden tablets which were placed as offerings at Shinto shrines or Buddhist temples during the Edo period (1603–1867) by members of all social classes.
Contents |
History
The Sangaku were painted in color on wooden tablets and hung in the precincts of Buddhist temples and Shinto shrines as offerings to the gods or as challenges to the congregants or publish what question one solved. Many of these tablets were lost during the period of modernization that followed the Edo period, but around nine hundred are known to remain.
Fujita Kagen (1765–1821), a Japanese mathematician of prominence, published the first collection of sangaku problems, his Shimpeki Sampo (Mathematical problems Suspended from the Temple) in 1790, and in 1806 a sequel, the Zoku Shimpeki Sampo.
During this period Japan applied strict regulations to commerce and foreign relations for western countries so the tablets were created using Japanese mathematics, (wasan), developed in parallel to western mathematics. For example, the connection between an integral and its derivative (the fundamental theorem of calculus) was unknown, so Sangaku problems on areas and volumes were solved by expansions in infinite series and term-by-term calculation.
Select examples
A typical problem, which is presented on an 1824 tablet in the Gunma Prefecture, covers the relationship of three touching circles with a common tangent. Given the size of the two outer large circles, what is the size of the small circle between them? The answer is:
(See also Ford circle.)
In the west
Soddy's hexlet, thought previously to have been discovered in the west in 1937, has been discovered on a Sangaku dating from 1822.
See also
- Recreational mathematics
- Seki Takakazu
- Japanese theorem for concyclic polygons
- Japanese theorem for concyclic quadrilaterals
- Equal Incircles Theorem
Notes
References
- Fukagawa, Hidetoshi, and Dan Pedoe. (1989). Japanese temple geometry problems = Sangaku. Winnipeg: Charles Babbage. 10-ISBN 0919611214/13-ISBN 9780919611214; OCLC 474564475
- __________ and Dan Pedoe. (1991) How to resolve Japanese temple geometry problems? (日本の幾何ー何題解けますか? Nihon no kika nan dai tokemasu ka) Tōkyō : Mori Kitashuppan. 10-ISBN 4627015305/13-ISBN 9784627015302; OCLC 47500620
- __________ and Tony Rothman. (2008). Sacred Mathematics: Japanese Temple Geometry. Princeton: Princeton University Press. 10-ISBN 9780691127453/13-ISBN 069112745X; OCLC 181142099
- Huvent, Géry. (2008). Sangaku. Le mystère des énigmes géométriques japonaises. Paris: Dunod. 13-ISBN 9782100520305/10-ISABN 210052030X; OCLC 470626755
- Rehmeyer, Julie, "Sacred Geometry", Science News, March 21, 2008.
- Rothman, Tony and Fugakawa, Hidetoshi. "Japanese Temple Geometry," Scientific American, May 1998.