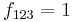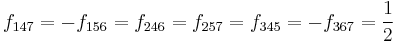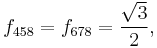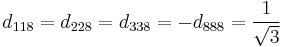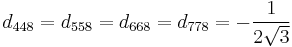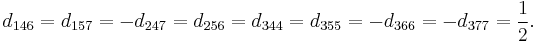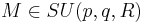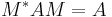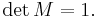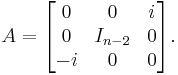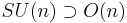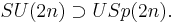Special unitary group
| Group theory |
|---|
| Group theory |
|
Cyclic group Zn
Symmetric group, Sn Dihedral group, Dn Alternating group An Mathieu groups M11, M12, M22, M23, M24 Conway groups Co1, Co2, Co3 Janko groups J1, J2, J3, J4 Fischer groups F22, F23, F24 Baby Monster group B Monster group M |
|
|
|
Solenoid (mathematics)
Circle group General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) Lorentz group Poincaré group Conformal group Diffeomorphism group Loop group Infinite-dimensional Lie groups O(∞) SU(∞) Sp(∞) |
| Lie groups |
|---|
|
General linear group GL(n)
Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) |
The special unitary group of degree n, denoted SU(n), is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication. The special unitary group is a subgroup of the unitary group U(n), consisting of all n×n unitary matrices, which is itself a subgroup of the general linear group GL(n, C).
The SU(n) groups find wide application in the Standard Model of particle physics, especially SU(2) in the electroweak interaction and SU(3) in QCD.
The simplest case, SU(1), is the trivial group, having only a single element. The group SU(2) is isomorphic to the group of quaternions of norm 1, and is thus diffeomorphic to the 3-sphere. Since unit quaternions can be used to represent rotations in 3-dimensional space (up to sign), we have a surjective homomorphism from SU(2) to the rotation group SO(3) whose kernel is 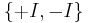 .
.
Contents |
Properties
The special unitary group SU(n) is a real matrix Lie group of dimension n² - 1. Topologically, it is compact and simply connected. Algebraically, it is a simple Lie group (meaning its Lie algebra is simple; see below). The center of SU(n) is isomorphic to the cyclic group Zn. Its outer automorphism group, for n ≥ 3, is Z2, while the outer automorphism group of SU(2) is the trivial group.
The Lie algebra of SU(n), denoted by 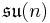 is generated by n² operators, which satisfy the commutator relationship (for i,j,k,l = 1, 2, ..., n)
is generated by n² operators, which satisfy the commutator relationship (for i,j,k,l = 1, 2, ..., n)
Additionally, the operator
satisfies
which implies that the number of independent generators is n²-1.[1]
Generators
In general the infinitesimal generators (functions generative of the infinitesimal) of SU(n), T, are represented as traceless hermitian matrices. I.e:
and
Fundamental representation
In the defining or fundamental representation the generators are represented by n×n matrices where:
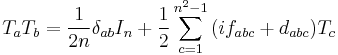
- where the f are the structure constants and are antisymmetric in all indices, whilst the d are symmetric in all indices.
As a consequence:
We also have
as a normalization convention.
Adjoint representation
In the adjoint representation the generators are represented by n²-1 × n²-1 matrices, n²-1 of them, whose elements are defined by the structure constants:
n=2
SU(2) is the following group:
Now consider the following map:
where 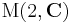 denotes the set of 2 by 2 complex matrices. By considering
denotes the set of 2 by 2 complex matrices. By considering 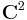 diffeomorphic to
diffeomorphic to 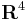 and
and 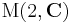 diffeomorphic to
diffeomorphic to 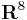 we can see that
we can see that  is an injective real linear map and hence an embedding. Now considering the restriction of
is an injective real linear map and hence an embedding. Now considering the restriction of  to the 3-sphere, denoted
to the 3-sphere, denoted 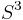 , we can see that this is an embedding of the 3-sphere onto a compact submanifold of
, we can see that this is an embedding of the 3-sphere onto a compact submanifold of 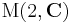 . However it is also clear that
. However it is also clear that 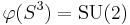 . Therefore as a manifold
. Therefore as a manifold 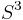 is diffeomorphic to SU(2) and so SU(2) is a compact, connected Lie group.
is diffeomorphic to SU(2) and so SU(2) is a compact, connected Lie group.
The Lie algebra of SU(2) is:
It is easily verified that matrices of this form have trace zero and are antihermitian. The Lie algebra is then generated by the following matrices
which are easily seen to have the form of the general element specified above. These satisfy the relations 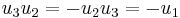 and
and 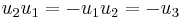 . The commutator bracket is therefore specified by
. The commutator bracket is therefore specified by
The above generators are related to the Pauli matrices by 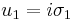 ,
, 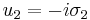 and
and 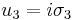 . This representation is often used in quantum mechanics (see Pauli matrices and Gell-Mann matrices), to represent the spin of fundamental particles such as electrons. They also serve as unit vectors for the description of our 3 spatial dimensions in quantum relativity.
. This representation is often used in quantum mechanics (see Pauli matrices and Gell-Mann matrices), to represent the spin of fundamental particles such as electrons. They also serve as unit vectors for the description of our 3 spatial dimensions in quantum relativity.
n=3
The generators of 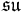 (3), T, in the defining representation, are:
(3), T, in the defining representation, are:
where 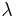 , the Gell-Mann matrices, are the SU(3) analog of the Pauli matrices for SU(2):
, the Gell-Mann matrices, are the SU(3) analog of the Pauli matrices for SU(2):
Note that they span all traceless Hermitian matrices as required.
These obey the relations
where the f are the structure constants, as previously defined, and have values given by
and all other 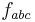 not related to these by permutation are zero.
not related to these by permutation are zero.
The d take the values:
Lie algebra
The Lie algebra corresponding to SU(n) is denoted by 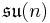 . Its standard mathematical representation consists of the traceless antihermitian
. Its standard mathematical representation consists of the traceless antihermitian 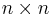 complex matrices, with the regular commutator as Lie bracket. A factor i is often inserted by particle physicists, so that all matrices become Hermitian. This is simply a different, more convenient, representation of the same real Lie algebra. Note that
complex matrices, with the regular commutator as Lie bracket. A factor i is often inserted by particle physicists, so that all matrices become Hermitian. This is simply a different, more convenient, representation of the same real Lie algebra. Note that 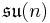 is a Lie algebra over R.
is a Lie algebra over R.
If we choose an (arbitrary) particular basis, then the subspace of traceless diagonal 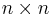 matrices with imaginary entries forms an
matrices with imaginary entries forms an 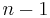 dimensional Cartan subalgebra.
dimensional Cartan subalgebra.
Complexify the Lie algebra, so that any traceless 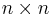 matrix is now allowed. The weight eigenvectors are the Cartan subalgebra itself and the matrices with only one nonzero entry which is off diagonal. Even though the Cartan subalgebra
matrix is now allowed. The weight eigenvectors are the Cartan subalgebra itself and the matrices with only one nonzero entry which is off diagonal. Even though the Cartan subalgebra 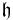 is only n - 1 dimensional, to simplify calculations, it is often convenient to introduce an auxiliary element, the unit matrix which commutes with everything else (which should not be thought of as an element of the Lie algebra!) for the purpose of computing weights and that only. So, we have a basis where the i-th basis vector is the matrix with 1 on the i-th diagonal entry and zero elsewhere. Weights would then be given by n coordinates and the sum over all n coordinates has to be zero (because the unit matrix is only auxiliary).
is only n - 1 dimensional, to simplify calculations, it is often convenient to introduce an auxiliary element, the unit matrix which commutes with everything else (which should not be thought of as an element of the Lie algebra!) for the purpose of computing weights and that only. So, we have a basis where the i-th basis vector is the matrix with 1 on the i-th diagonal entry and zero elsewhere. Weights would then be given by n coordinates and the sum over all n coordinates has to be zero (because the unit matrix is only auxiliary).
So, SU(n) is of rank n - 1 and its Dynkin diagram is given by 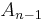 , a chain of
, a chain of 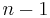 vertices. Its root system consists of n(n - 1) roots spanning a n - 1 Euclidean space. Here, we use n redundant coordinates instead of n - 1 to emphasize the symmetries of the root system (the n coordinates have to add up to zero). In other words, we are embedding this n - 1 dimensional vector space in an n-dimensional one. Then, the roots consists of all the n(n - 1) permutations of (1, -1, 0, ..., 0). The construction given two paragraphs ago explains why. A choice of simple roots is
vertices. Its root system consists of n(n - 1) roots spanning a n - 1 Euclidean space. Here, we use n redundant coordinates instead of n - 1 to emphasize the symmetries of the root system (the n coordinates have to add up to zero). In other words, we are embedding this n - 1 dimensional vector space in an n-dimensional one. Then, the roots consists of all the n(n - 1) permutations of (1, -1, 0, ..., 0). The construction given two paragraphs ago explains why. A choice of simple roots is
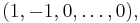
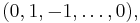
- …,

Its Cartan matrix is
Its Weyl group or Coxeter group is the symmetric group 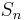 , the symmetry group of the (n - 1)-simplex.
, the symmetry group of the (n - 1)-simplex.
Generalized special unitary group
For a field F, the generalized special unitary group over F, SU(p,q;F), is the group of all linear transformations of determinant 1 of a vector space of rank n = p + q over F which leave invariant a nondegenerate, Hermitian form of signature (p, q). This group is often referred to as the special unitary group of signature p q over F. The field F can be replaced by a commutative ring, in which case the vector space is replaced by a free module.
Specifically, fix a Hermitian matrix A of signature p q in GL(n,R), then all
satisfy
Often one will see the notation 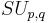 without reference to a ring or field, in this case the ring or field being referred to is C and this gives one of the classical Lie groups. The standard choice for A when F = C is
without reference to a ring or field, in this case the ring or field being referred to is C and this gives one of the classical Lie groups. The standard choice for A when F = C is
However there may be better choices for A for certain dimensions which exhibit more behaviour under restriction to subrings of C.
Example
A very important example of this type of group is the Picard modular group SU(2,1;Z[i]) which acts (projectively) on complex hyperbolic space of degree two, in the same way that SL(2,Z) acts (projectively) on real hyperbolic space of dimension two. In 2003 Gábor Francsics and Peter Lax computed a fundamental domain for the action of this group on 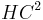 , see.[2] Another example is SU(1,1;C) which is isomorphic to SL(2,R).
, see.[2] Another example is SU(1,1;C) which is isomorphic to SL(2,R).
Important subgroups
In physics the special unitary group is used to represent bosonic symmetries. In theories of symmetry breaking it is important to be able to find the subgroups of the special unitary group. Subgroups of SU(n) that are important in GUT physics are, for p>1, n-p>1:
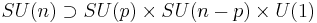 ,
,
where 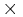 denotes the direct product and
denotes the direct product and 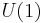 , known as the circle group, is the multiplicative group of all complex numbers with absolute value 1.
, known as the circle group, is the multiplicative group of all complex numbers with absolute value 1.
For completeness there are also the orthogonal and symplectic subgroups:
Since the rank of SU(n) is n-1 and of U(1) is 1, a useful check is that the sum of the ranks of the subgroups is less than or equal to the rank of the original group. SU(n) is a subgroup of various other lie groups:
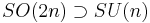
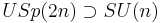
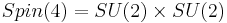 (see Spin group)
(see Spin group)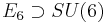
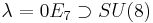
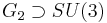 (see Simple Lie groups for E6, E7, and G2).
(see Simple Lie groups for E6, E7, and G2).
There are also the identities SU(4)=Spin(6), SU(2)=Spin(3)=USp(2) and U(1)=Spin(2)=SO(2) .
One should finally mention that SU(2) is the double covering group of SO(3), a relation that plays an important role in the theory of rotations of 2-spinors in non-relativistic quantum mechanics.
See also
Notes
- ^ R.R. Puri, Mathematical Methods of Quantum Optics, Springer, 2001.
- ^ http://www.esi.ac.at/Preprint-shadows/esi1273.html
References
- Halzen, Francis; Martin, Alan (1984). Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2.
- Maximal Subgroups of Compact Lie Groups
![\left [ \hat{O}_{ij} , \hat{O}_{kl} \right ] = \delta_{jk} \hat{O}_{il} - \delta_{il} \hat{O}_{kj}.](/2012-wikipedia_en_all_nopic_01_2012/I/2b88a95b2678949137c6857779228f25.png)
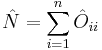
![\left [ \hat{N}, \hat{O}_{ij} \right ] = 0](/2012-wikipedia_en_all_nopic_01_2012/I/a56a3b2194863e2eb6459a1e883174e9.png)
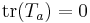
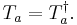
![\left[T_a, T_b\right]_%2B = \frac{1}{n}\delta_{ab} I_n%2B \sum_{c=1}^{n^2 -1}{d_{abc} T_c} \,](/2012-wikipedia_en_all_nopic_01_2012/I/a2256bc18c687fee59fc1f2a24698ca8.png)
![\left[T_a, T_b \right]_- = i \sum_{c=1}^{n^2 -1}{f_{abc} T_c}. \,](/2012-wikipedia_en_all_nopic_01_2012/I/f9a5cc33644a65f7a54d205c6da54ddb.png)
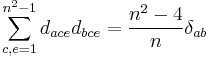
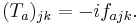
![[u_3,u_1]=2u_2, \qquad [u_1,u_2] = 2u_3, \qquad [u_2,u_3] = 2u_1.](/2012-wikipedia_en_all_nopic_01_2012/I/0f162905d8ce6f8ade5d63b8df44745e.png)
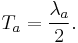
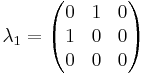
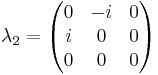
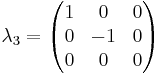
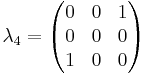
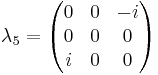
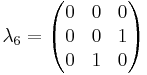
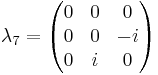
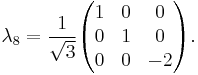
![\left[T_a, T_b \right] = i \sum_{c=1}^8{f_{abc} T_c} \,](/2012-wikipedia_en_all_nopic_01_2012/I/6ac31bf1e2e223ef47e0bb9ad00842ea.png)