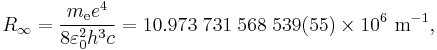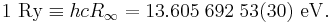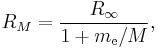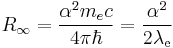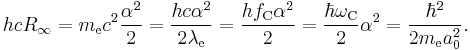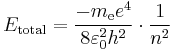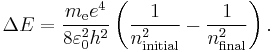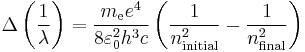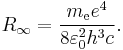Rydberg constant

The Rydberg constant, symbol R_∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated from more fundamental constants by using quantum mechanics. As of 2010, it is the most accurately measured fundamental physical constant.^[1]

The Rydberg constant represents the limiting value of the highest wavenumber (the inverse wavelength) of any photon that can be emitted from the hydrogen atom, or, alternatively, the wavenumber of the lowest-energy photon capable of ionizing the hydrogen atom from its ground state. The spectrum of hydrogen can be expressed simply in terms of the Rydberg constant, using the Rydberg formula.

The Rydberg unit of energy, symbol Ry, is closely related to the Rydberg constant. It corresponds to the energy of the photon whose wavenumber is the Rydberg constant, i.e. the ionization energy of the hydrogen atom.

1 Value of the Rydberg constant and Rydberg unit of energy
2 Measurement
3 Alternative expressions
4 The derivation of Rydberg constant from quantum mechanics
5 See also
6 References

Value of the Rydberg constant and Rydberg unit of energy

Making use of the simplifying assumption that the mass of the atomic nucleus is infinite compared to the mass of the electron,^[2] so that the center of mass of the system lies at the barycenter of the nucleus, according to the 2010 CODATA the constant is:

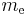$R_\infty = \frac{m_{\mathrm{e}} e^4}{8 \varepsilon_0^2 h^3 c} = 10.973\;731\;568\;539(55) \times 10^6 \ \mathrm{m}^{-1},$ ^[3]

where $m_{\mathrm{e}}$ is the rest mass of the electron, $e$ is the elementary charge, 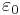$\varepsilon_0$ is the permittivity of free space, $h$ is the Planck constant, and $c$ is the speed of light in a vacuum.

This constant is often used in atomic physics in the form of the Rydberg unit of energy:

$1 \ \mathrm{Ry} \equiv h c R_\infty = 13.605\;692\;53(30) \ \mathrm{eV}.$ ^[3]

Two complications arise. One is that one may wish to discuss a hydrogen-like ion; that is, an atom with atomic number Z that has only one electron, such as C⁵⁺. In this case, the wavenumbers and photon energies are scaled up by a factor of Z², neglecting relativistic effects. The other is that the mass of the atomic nucleus is not actually infinite compared to the mass of the electron. The predicted spectrum must then be corrected by substituting the reduced mass for the mass of the electron. The Rydberg constant R_M for an atom with one electron is then given by

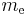$R_M = \frac{R_\infty}{1%2Bm_{\mathrm{e}}/M},$

where $m_{\mathrm{e}}$ is the rest mass of the electron, and M is the mass of the atomic nucleus.

Measurement

The Rydberg constant is the most well-determined physical constant, with a relative experimental uncertainty of less than 7 parts in 10¹². The ability to measure it to such a high precision constrains the proportions of the values of the other physical constants that define it.^[3] See precision tests of QED.

The Rydberg constant 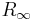$R_{\infty}$ is defined by the spectrum that a hydrogen atom would have if its nucleus was infinitely massive, if there was no fine structure or hyperfine splitting, and so on. Therefore it cannot be directly measured at very high accuracy from the atomic transition frequencies of hydrogen alone. Instead, the Rydberg constant is inferred from measurements of atomic transition frequencies in three different atoms (hydrogen, deuterium, and antiprotonic helium). Detailed theoretical calculations in the framework of quantum electrodynamics are used to account for the effects of finite nuclear mass, fine structure, hyperfine splitting, and so on. Finally, the value of 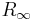$R_{\infty}$ comes from the best fit of the measurements to the theory.^[4]

Alternative expressions

The Rydberg constant can also be expressed as the following equations.

$R_\infty = \frac{\alpha^2 m_e c}{4 \pi \hbar} = \frac{\alpha^2}{2 \lambda_{\mathrm{e}}} \$

and

$h c R_\infty = m_{\mathrm{e}} c^2 \frac{\alpha^2}{2} = \frac{h c \alpha^2}{2 \lambda_{\mathrm{e}}} = \frac{h f_{\mathrm{C}} \alpha^2}{2} = \frac{\hbar \omega_{\mathrm{C}}}{2} \alpha^2 = \dfrac{\hbar^2}{2m_{\mathrm{e}}a_0^2}.$

where

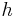$h\!$ is the Planck constant

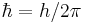$\hbar= h/2\pi$ is the reduced Planck constant,

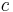$c\!$ is the speed of light in a vacuum,

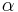$\alpha\!$ is the fine-structure constant,

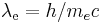$\lambda_{\mathrm{e}} = h/m_e c\!$ is the Compton wavelength of the electron,

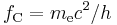$f_{\mathrm{C}}=m_{\mathrm{e}} c^2/h\!$ is the Compton frequency of the electron,

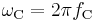$\omega_{\mathrm{C}}=2\pi f_{\mathrm{C}}\!$ is the Compton angular frequency of the electron,

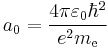$a_0=\frac{4\pi\varepsilon_0\hbar^2}{e^2m_{\mathrm{e}}}$ is the Bohr radius.

The second equation is relevant because it is the coefficient for the energy of the atomic orbitals of a hydrogen atom: 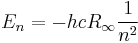$E_n = -h c R_\infty \frac{1}{n^2}$ .

The derivation of Rydberg constant from quantum mechanics

Historically, the Rydberg formula was found empirically (experimentally), and it predated the development of quantum theory. To understand its significance in terms of the quantum theory, we can start from the equation

$E_\mathrm{total} = \frac{- m_{\mathrm{e}} e^4}{8 \varepsilon_0^2 h^2} \cdot \frac{1}{n^2} \$

for the energy of an atom with one electron and a nucleus with a charge of +1 and an infinite mass. Of course, atomic nuclei do not have infinite masses in real life, but even the lightest nucleus, a single proton, is over 1800 times heavier than an electron, so this is reasonable as a first approximation. This energy formula can be derived either from the Bohr model or from a fully quantum-mechanical treatment of a hydrogen-like atom. Therefore the change in energy due to the electron changing from one value of $n$ to another is

$\Delta E = \frac{ m_{\mathrm{e}} e^4}{8 \varepsilon_0^2 h^2} \left( \frac{1}{n_\mathrm{initial}^2} - \frac{1}{n_\mathrm{final}^2} \right). \$

We simply change the units to wavenumbers 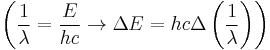$\left( \frac{1}{ \lambda} = \frac {E}{hc} \rightarrow \Delta{E} = hc \operatorname{\Delta} \left( \frac{1}{\lambda}\right)\right) \$ and we get

$\Delta \left( \frac{1}{ \lambda}\right) = \frac{ m_{\mathrm{e}} e^4}{8 \varepsilon_0^2 h^3 c} \left( \frac{1}{n_\mathrm{initial}^2} - \frac{1}{n_\mathrm{final}^2} \right) \$

where

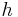$h \$ is Planck's constant,

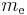$m_{\mathrm{e}} \$ is the rest mass of the electron,

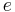$e \$ is the elementary charge,

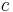$c \$ is the speed of light in vacuum, and

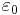$\varepsilon_0 \$ is the permittivity of free space.

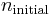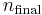$n_\mathrm{initial} \$ and $n_\mathrm{final} \$ being the electron shell number of the hydrogen atom.

We have therefore found the Rydberg constant for our hypothetical system of a nucleus with infinite mass, a +1 charge, and a single electron to be

$R_\infty = \frac{ m_{\mathrm{e}} e^4}{8 \varepsilon_0^2 h^3 c}.$

References

^ Pohl, Randolf; Antognini, Aldo; Nez, François; Amaro, Fernando D.; Biraben, François; Cardoso, João M. R.; Covita, Daniel S.; Dax, Andreas et al. (2010). "The size of the proton". Nature 466 (7303): 213–216. Bibcode 2010Natur.466..213P. doi:10.1038/nature09250. PMID 20613837.
^ Coffman, Moody L. (1965). "Correction to the Rydberg Constant for Finite Nuclear Mass". American Journal of Physics 33 (10): 820–823. Bibcode 1965AmJPh..33..820C. doi:10.1119/1.1970992.
^ ^a ^b ^c P.J. Mohr, B.N. Taylor, and D.B. Newell (2011), "The 2010 CODATA Recommended Values of the Fundamental Physical Constants" (Web Version 6.0). This database was developed by J. Baker, M. Douma, and S. Kotochigova. Available: http://physics.nist.gov/constants. National Institute of Standards and Technology, Gaithersburg, MD 20899. Link to R_∞, Link to hcR_∞
^ Mohr, P. J.; taylor, B. N.; Newell, D. B. (2008). "CODATA recommended values of the fundamental physical constants: 2006". Reviews of Modern Physics 80 (2): 633–730. Bibcode 2008RvMP...80..633M. doi:10.1103/RevModPhys.80.633.