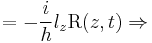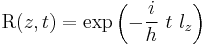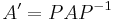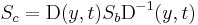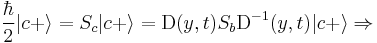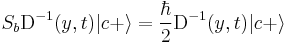Rotation operator (quantum mechanics)
This article concerns the rotation operator, as it appears in quantum mechanics.
Contents |
The translation operator
The rotation operator 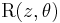 , with the first argument
, with the first argument 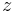 indicating the rotation axis and the second
indicating the rotation axis and the second 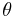 the rotation angle, can operate through the translation operator
the rotation angle, can operate through the translation operator 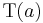 for infinitesimal rotations as explained below. This is why, it is first shown how the translation operator is acting on a particle at position x (the particle is then in the state
for infinitesimal rotations as explained below. This is why, it is first shown how the translation operator is acting on a particle at position x (the particle is then in the state 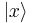 according to Quantum Mechanics).
according to Quantum Mechanics).
Translation of the particle at position x to position x+a: 
Because a translation of 0 does not change the position of the particle, we have (with 1 meaning the identity operator, which does nothing):
Taylor development gives:
with
From that follows:
This is a differential equation with the solution 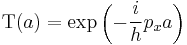 .
.
Additionally, suppose a Hamiltonian 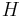 is independent of the
is independent of the 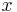 position. Because the translation operator can be written in terms of
position. Because the translation operator can be written in terms of 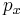 , and
, and ![\,[p_x,H]=0](/2012-wikipedia_en_all_nopic_01_2012/I/8fb73e060728bb21ce7de3f78b70238a.png) , we know that
, we know that ![\,[H,\mbox{T}(a)]=0](/2012-wikipedia_en_all_nopic_01_2012/I/c6be1d348bd41ad6b17f6f1becf5e47f.png) . This result means that linear momentum for the system is conserved.
. This result means that linear momentum for the system is conserved.
In relation to the orbital angular momentum
Classically we have for the angular momentum 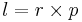 . This is the same in quantum mechanics considering
. This is the same in quantum mechanics considering 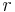 and
and 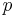 as operators. Classically, an infinitesimal rotation
as operators. Classically, an infinitesimal rotation 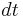 of the vector r=(x,y,z) about the z-axis to r'=(x',y',z) leaving z unchanged can be expressed by the following infinitesimal translations (using Taylor approximation):
of the vector r=(x,y,z) about the z-axis to r'=(x',y',z) leaving z unchanged can be expressed by the following infinitesimal translations (using Taylor approximation):
From that follows for states:
And consequently:
Using 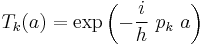 from above with
from above with 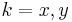 and Taylor development we get:
and Taylor development we get:
with lz = x py - y px the z-component of the angular momentum according to the classical cross product.
To get a rotation for the angle 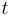 , we construct the following differential equation using the condition
, we construct the following differential equation using the condition 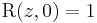 :
:
Similar to the translation operator, if we are given a Hamiltonian 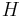 which rotationally symmetric about the z axis,
which rotationally symmetric about the z axis, ![\,[l_z,H]=0](/2012-wikipedia_en_all_nopic_01_2012/I/685da2b7d2200f6e94f2e206d082f0fe.png) implies
implies ![\,[\mbox{R}(z,t),H]=0](/2012-wikipedia_en_all_nopic_01_2012/I/28fcaec52b7800bfe795410b487b8cbd.png) . This result means that angular momentum is conserved.
. This result means that angular momentum is conserved.
For the spin angular momentum about the y-axis we just replace 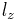 with
with 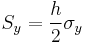 and we get the spin rotation operator
and we get the spin rotation operator 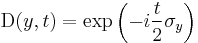 .
.
Effect upon the spin operator and upon states
Operators can be represented by matrices. From linear algebra one knows that a certain matrix 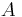 can be represented in another basis through the transformation
can be represented in another basis through the transformation
where 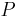 is the basis transformation matrix. If the vectors
is the basis transformation matrix. If the vectors 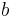 respectively
respectively 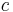 are the z-axis in one basis respectively another, they are perpendicular to the y-axis with a certain angle
are the z-axis in one basis respectively another, they are perpendicular to the y-axis with a certain angle 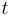 between them. The spin operator
between them. The spin operator 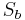 in the first basis can then be transformed into the spin operator
in the first basis can then be transformed into the spin operator 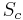 of the other basis through the following transformation:
of the other basis through the following transformation:
From standard quantum mechanics we have the known results 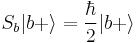 and
and 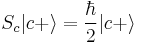 where
where 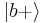 and
and 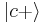 are the top spins in their corresponding bases. So we have:
are the top spins in their corresponding bases. So we have:
Comparison with 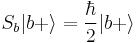 yields
yields 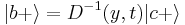 .
.
This means that if the state 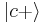 is rotated about the y-axis by an angle
is rotated about the y-axis by an angle 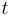 , it becomes the state
, it becomes the state 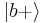 , a result that can be generalized to arbitrary axes. It is important, for instance, in Sakurai's Bell inequality.
, a result that can be generalized to arbitrary axes. It is important, for instance, in Sakurai's Bell inequality.
References
- L.D. Landau and E.M. Lifshitz: Quantum Mechanics: Non-Relativistic Theory, Pergamon Press, 1985
- P.A.M. Dirac: The Principles of Quantum Mechanics, Oxford University Press, 1958
- R.P. Feynmann, R.B. Leighton and M. Sands: The Feynmann Lectures on Physics, Addison-Wesley, 1965
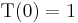
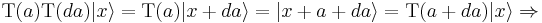
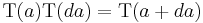
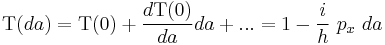
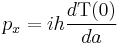
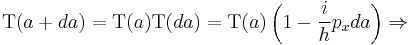
![\,[\mbox{T}(a %2B da) - \mbox{T}(a)]/da = \frac{d\mbox{T}}{da} = - \frac{i}{h} p_x \mbox{T}(a)](/2012-wikipedia_en_all_nopic_01_2012/I/439a449fa9b85f501ef9762f96c84762.png)
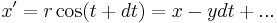
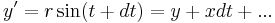
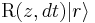
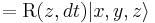
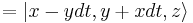
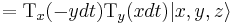
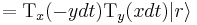
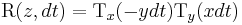
![\,\mbox{R}(z, dt) = \exp\left[- \frac{i}{h}\ (x p_y - y p_x) dt\right]](/2012-wikipedia_en_all_nopic_01_2012/I/4cff3884f7ddb4aa906bb572cf4fb46f.png)
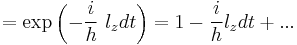
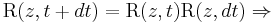
![\,[\mbox{R}(z, t %2B dt) - \mbox{R}(z, t)]/dt = d\mbox{R}/dt](/2012-wikipedia_en_all_nopic_01_2012/I/39bc484cb3c9a632360fd90cc76464e4.png)
![\,= \mbox{R}(z, t) [\mbox{R}(z, dt) - 1]/dt](/2012-wikipedia_en_all_nopic_01_2012/I/f981ada663794d72cf926b4372711cae.png)