Risk measure
A Risk measure is used to determine the amount of an asset or set of assets (traditionally currency) to be kept in reserve. The purpose of this reserve is to make the risks taken by financial institutions, such as banks and insurance companies, acceptable to the regulator. In recent years attention has turned towards convex and coherent risk measurement.
Contents[hide] |
Mathematically
A risk measure is defined as a mapping from a set of random variables to the real numbers. This set of random variables represents the risk at hand. The common notation for a risk measure associated with a random variable  is
is ![\rho[X]](/2012-wikipedia_en_all_nopic_01_2012/I/b9901c749033b10a87319ffa5d0e98fd.png) . A risk measure
. A risk measure 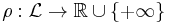 should have certain properties:
should have certain properties:
- Normalized
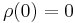
- Translative
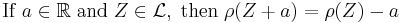
- Monotone
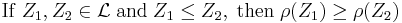
Set-valued
In a situation with 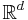 -valued portfolios such that risk can be measured in
-valued portfolios such that risk can be measured in 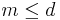 of the assets, then a set of portfolios is the proper way to depict risk. Set-valued risk measures are useful for markets with transaction costs.[1]
of the assets, then a set of portfolios is the proper way to depict risk. Set-valued risk measures are useful for markets with transaction costs.[1]
Mathematically
A set-valued risk measure is a function 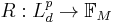 , where
, where 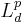 is a
is a  -dimensional Lp space,
-dimensional Lp space, 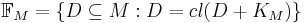 , and
, and 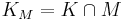 where
where  is a constant solvency cone and
is a constant solvency cone and  is the set of portfolios of the
is the set of portfolios of the  reference assets.
reference assets.  must have the following properties:[2]
must have the following properties:[2]
- Normalized
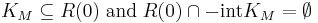
- Translative in M
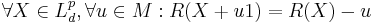
- Monotone
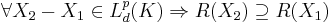
Examples
Well known risk measures
- Value at risk
- Expected shortfall
- Tail conditional expectation
- Entropic risk measure
- Superhedging price
- ...
Variance
Variance (or standard deviation) is not a risk measure. This can be seen since it has neither the translation property or monotonicity. That is 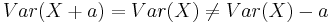 for all
for all 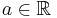 , and a simple counterexample for monotonicity can be found. The standard deviation is a deviation risk measure.
, and a simple counterexample for monotonicity can be found. The standard deviation is a deviation risk measure.
Relation to Acceptance Set
There is a one-to-one correspondence between an acceptance set and a corresponding risk measure. As defined below it can be shown that 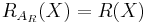 and
and 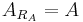 .
.
Risk Measure to Acceptance Set
- If
 is a (scalar) risk measure then
is a (scalar) risk measure then 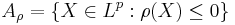 is an acceptance set.
is an acceptance set. - If
 is a set-valued risk measure then
is a set-valued risk measure then 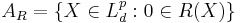 is an acceptance set.
is an acceptance set.
Acceptance Set to Risk Measure
- If
 is an acceptance set (in 1-d) then
is an acceptance set (in 1-d) then 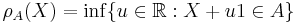 defines a (scalar) risk measure.
defines a (scalar) risk measure. - If
 is an acceptance set then
is an acceptance set then 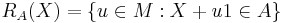 is a set-valued risk measure.
is a set-valued risk measure.
Relation with deviation risk measure
There is a one-to-one relationship between a deviation risk measure D and an expectation-bounded risk measure  where for any
where for any 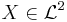
![D(X) = \rho(X - \mathbb{E}[X])](/2012-wikipedia_en_all_nopic_01_2012/I/f30cf3990e36fd3608d4c0401378f175.png)
![\rho(X) = D(X) - \mathbb{E}[X]](/2012-wikipedia_en_all_nopic_01_2012/I/584ed007620df7b2a04f0da18c6a949d.png) .
.
 is expectation bounded if
is expectation bounded if ![\rho(X) > \mathbb{E}[-X]](/2012-wikipedia_en_all_nopic_01_2012/I/a7795d7e4730e72fa0f4d899d07ed88f.png) for any nonconstant X and
for any nonconstant X and ![\rho(X) = \mathbb{E}[-X]](/2012-wikipedia_en_all_nopic_01_2012/I/333bbe7f31e3642b13af07ea5e73af5e.png) for any constant X.[3]
for any constant X.[3]
See also
Further reading
- Crouhy, Michel; D. Galai, and R. Mark (2001). Risk Management. McGraw-Hill. pp. 752 pages. ISBN 0-07-135731-9.
- Kevin, Dowd (2005). Measuring Market Risk (2nd ed.). John Wiley & Sons. pp. 410 pages. ISBN 0-470-01303-6.
References
- ^ Jouini, Elyes; Meddeb, Moncef; Touzi, Nizar (2004). "Vector–valued coherent risk measures". Finance and Stochastics 8 (4): 531–552.
- ^ Hamel, Andreas; Heyde, Frank (December 11, 2008) (pdf). Duality for Set-Valued Risk Measures. http://www.princeton.edu/~ahamel/SetRiskHamHey.pdf. Retrieved July 22, 2010.
- ^ Rockafellar, Tyrrell; Uryasev, Stanislav; Zabarankin, Michael (2002) (pdf). Deviation Measures in Risk Analysis and Optimization. http://www.ise.ufl.edu/uryasev/Deviation_measures_wp.pdf. Retrieved October 13, 2011.}}