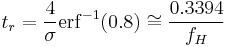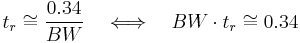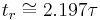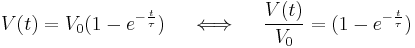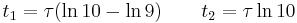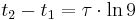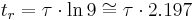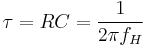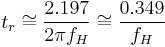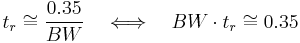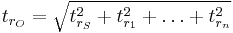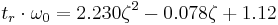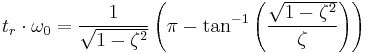Rise time
In electronics, when describing a voltage or current step function, rise time refers to the time required for a signal to change from a specified low value to a specified high value. Typically, in analog electronics, these values are 10% and 90% of the step height: in control theory applications, according to Levine (1996, p. 158), rise time is defined as "the time required for the response to rise from x% to y% of its final value", with 0%-100% rise time common for underdamped second order systems, 5%-95% for critically damped and 10%-90% for overdamped.[1] The output signal of a system is characterized also by fall time: both parameters depend on rise and fall times of input signal and on the characteristics of the system.
Contents |
Overview
Rise time is an analog parameter of fundamental importance in high speed electronics, since it is a measure of the ability of a circuit to respond to fast input signals. Many efforts over the years have been made to reduce the rise times of generators, analog and digital circuits, measuring and data transmission equipment, focused on the research of faster electron devices and on techniques of reduction of stray circuit parameters (mainly capacitances and inductances). For applications outside the realm of high speed electronics, long (compared to the attainable state of the art) rise times are sometimes desirable: examples are the dimming of a light, where a longer rise-time results, amongst other things, in a longer life for the bulb, or digital signals apt to the control of analog ones, where a longer rise time means lower capacitive feedthrough, and thus lower coupling noise.
Simple examples of calculation of rise time
The aim of this section is the calculation of rise time of step response for some simple systems: all notations and assumptions required for the following analysis are listed here.
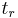 is the rise time of the analyzed system, measured in seconds.
is the rise time of the analyzed system, measured in seconds.
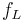 is the low frequency cutoff (-3 dB point) of the analyzed system, measured in hertz.
is the low frequency cutoff (-3 dB point) of the analyzed system, measured in hertz.
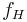 is high frequency cutoff (-3 dB point) of the analyzed system, measured in hertz.
is high frequency cutoff (-3 dB point) of the analyzed system, measured in hertz.
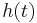 is the impulse response of the analyzed system in the time domain.
is the impulse response of the analyzed system in the time domain.
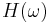 is the frequency response of the analyzed system in the frequency domain.
is the frequency response of the analyzed system in the frequency domain.
- The bandwidth is defined as
- and since the low frequency cutoff
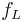 is usually several decades lower than the high frequency cutoff
is usually several decades lower than the high frequency cutoff 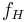 ,
,
- All systems analyzed here have a frequency response which extends to 0 (low-pass systems), thus
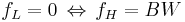 exactly.
exactly.
- All systems analyzed are thought as electrical networks and all the signals are thought as voltages for the sake of simplicity: the input is a step function of
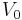 volts.
volts.
Gaussian response system
A system is said to have a Gaussian response if it is characterized by the following frequency response
where 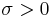 is a constant, related to the high frequency cutoff by the following relation:
is a constant, related to the high frequency cutoff by the following relation:
The corresponding impulse response can be calculated using the inverse Fourier transform of the shown frequency response
Applying directly the definition of step response
Solving for t's the two following equations by using known properties of the error function
the value 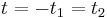 is then known and since
is then known and since 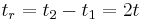
and then
One stage low pass RC network
For a simple one stage low pass  network, rise time is proportional to the network time constant
network, rise time is proportional to the network time constant 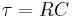 :
:
The proportionality constant can be derived by using the output response of the network to a step function input Signal (electrical engineering) of 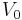 amplitude, aka its step response:
amplitude, aka its step response:
Solving for t's the two equations
the times 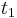 and
and 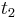 to 10% and 90% of steady-state value thus known
to 10% and 90% of steady-state value thus known
Subtracting 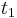 from
from 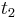
which is the rise time. Therefore rise time is proportional to the time constant:
Now, noting that
then
and since the high frequency cutoff is equal to the bandwidth
This formula implies that if the bandwidth of an oscilloscope is 350 MHz, its 10% to 90% risetime is 1 nanosecond.
Rise time of cascaded blocks
Consider a system composed by  cascaded non interacting blocks, each having a rise time
cascaded non interacting blocks, each having a rise time 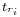 and no overshoot in their step response: suppose also that the input signal of the first block has a rise time whose value is
and no overshoot in their step response: suppose also that the input signal of the first block has a rise time whose value is 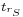 . Then its output signal has a rise time
. Then its output signal has a rise time 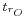 equal to
equal to
This result is a consequence of the central limit theorem, as reported in Valley & Wallman 1948, pp. 77–78 and proved by Henry Wallman in Wallman 1950.[2]
Factors affecting rise time
Rise time values in a resistive circuit are primarily due to stray capacitance and inductance in the circuit. Because every circuit has not only resistance, but also capacitance and inductance, a delay in voltage and/or current at the load is apparent until the steady state is reached. In a pure RC circuit, the output risetime (10% to 90%), as shown above, is approximately equal to 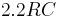 .
.
Rise time in control applications
In control theory, for overdamped systems, rise time is commonly defined as the time for a waveform to go from 10% to 90% of its final value.[1]
The quadratic approximation for normalized rise time for a 2nd-order system, step response, no zeros is:
where ζ is the damping ratio and ω0 is the natural frequency of the network.
However, the proper calculation for rise time from 0 to 100% of an under-damped 2nd-order system is:
where ζ is the damping ratio and ω0 is the natural frequency of the network.
See also
Notes
- ^ a b Precisely, Levine (1996, p. 158) states: "The rise time is the time required for the response to rise from x% to y% of its final value. For overdamped second order systems, the 0% to 100% rise time is normally used, and for underdamped systems...the 10% to 90% rise time is commonly used". See also the textbook Nise 2008.
- ^ This beautiful one-page paper does not contain any calculation. Henry Wallman simply sets up a table he calls dictionary paralleling concepts from electronics engineering and probability theory: the key of the process is the use of Laplace transform. Then he notes that, following the correspondence of concepts established by the dictionary, that the step response of a cascade of blocks corresponds to the central limit theorem and states that: "This has important practical consequences, among them the fact that if a network is free of overshoot its time-of-response inevitably increases rapidly upon cascading, namely as the square-root of the number of cascaded network".(Wallman 1950, p. 91)
References
- Levine, William S. (1996), The control handbook, Boca Raton, FL: CRC Press, pp. 1548, ISBN 0849385709.
- Nise, Norman S. (2008), Control Systems Engineering (Fifth ed.), John Wiley & Sons, pp. xvii+880, ISBN 978-0471-79475-2
- United States Federal Standard 1037C: Glossary of Telecommunications Terms
- Valley, George E., Jr.; Wallman, Henry (1948), Vacuum Tube Amplifiers, MIT Radiation Laboratory Series, 18, New York: McGraw-Hill., pp. xvii+743 Paragraph 2 of chapter 2 and paragraphs 1 to 7 of chapter 7 .
- Wallman, Henry (1950), "Transient response and the central limit theorem of probability", Proceedings of Symposia in Applied Mathematics (Providence: AMS.) 2: 91, MR0034250, Zbl 0035.08102.
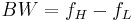
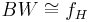
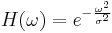
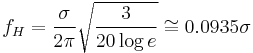
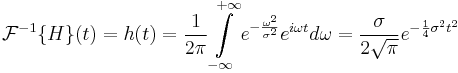
![V(t) = V_0{H*h}(t) = \frac{V_0}{\sqrt{\pi}}\int\limits_{-\infty}^{\frac{\sigma t}{2}}e^{-\tau^2}d\tau = \frac{V_0}{2}\left[1%2B\mathrm{erf}\left(\frac{\sigma t}{2}\right)\right]\Leftrightarrow\frac{V(t)}{V_0}=\frac{1}{2}\left[1%2B\mathrm{erf}\left(\frac{\sigma t}{2}\right)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/dcf959f587129272038d081070a42b4e.png)
![0.1=\frac{1}{2}\left[1%2B\mathrm{erf}\left(\frac{\sigma t_1}{2}\right)\right]
\qquad0.9=\frac{1}{2}\left[1%2B\mathrm{erf}\left(\frac{\sigma t_2}{2}\right)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/150058c6b37b15e91f60e5cbaf5a44d3.png)