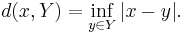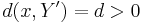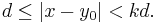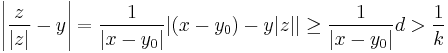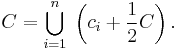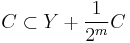Riesz's lemma
Riesz's lemma (after Frigyes Riesz) is a lemma in functional analysis. It specifies (often easy to check) conditions which guarantee that a subspace in a normed linear space is dense.
Contents |
The result
Before stating the result, we fix some notation. Let X be a normed linear space with norm |·| and x be an element of X. Let Y be a subspace in X. The distance between an element x and Y is defined by
Riesz's lemma reads as follows:
- Let X be a normed linear space and Y be a subspace in X. If there exists 0 < r < 1 such that for every x ∈ X with |x| =1, one has d(x, Y) < r, then Y is dense in X.
In other words, for every proper closed subspace Y, one can always find a vector x on the unit sphere of X such that d(x, Y) is less than and arbitrarily close to 1.
Proof: A simple proof can be sketched as follows. Suppose Y is not dense in X, therefore the closure of Y, denoted by Y' , is a proper subspace of X. Take an element x not in Y' , then we have
So, for any k > 1, there exists y0 in Y' such that
Consider the vector z = x - y0. We can calculate directly
for any y in Y. Choosing k arbitrarily close to 1 finishes the proof.
Note
For the finite dimensional case, equality can be achieved. In other words, there exists x of unit norm such that d(x, Y) is 1. When dimension of X is finite, the unit ball B ⊂ X is compact. Also, the distance function d(· , Y) is continuous. Therefore its image on the unit ball B must be a compact subset of the real line, and this proves the claim.
On the other hand, the example of the space 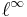 of all bounded sequences shows that the lemma does not hold for k = 1.
of all bounded sequences shows that the lemma does not hold for k = 1.
Converse
Riesz's lemma can be applied directly to show that the unit ball of an infinite-dimensional normed space X is never compact: Take an element x1 from the unit sphere. Pick xn from the unit sphere such that
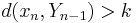 for a constant 0 < k < 1, where Yn-1 is the linear span of {x1 ... xn-1}.
for a constant 0 < k < 1, where Yn-1 is the linear span of {x1 ... xn-1}.
Clearly {xn} contains no convergent subsequence and the noncompactness of the unit ball follows.
The converse of this, in a more general setting, is also true. If a topological vector space X is locally compact, then it is finite dimensional. Therefore local compactness characterizes finite-dimensionality. This classical result is also attributed to Riesz. A short proof can be sketched as follows: let C be a compact neighborhood of 0 ∈ X. By compactness, there is c1 ... cn ∈ C such that
We claim that the finite dimensional subspace Y spanned by {ci}, or equivalently, its closure, is X. Since scalar multiplication is continuous, its enough to show C ⊂ Y. Now, by induction,
for every m. But compact sets are bounded, so C lies in the closure of Y. This proves the result.
Some consequences
The spectral properties of compact operators acting on a Banach space are similar to those of matrices. Riesz's lemma is essential in establishing this fact.
Riesz's lemma guarantees that any infinite-dimensional normed space contains a sequence of unit vectors 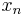 with
with 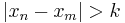 for 0 < k < 1. This is useful in showing the non-existence of certain measures on infinite-dimensional Banach spaces.
for 0 < k < 1. This is useful in showing the non-existence of certain measures on infinite-dimensional Banach spaces.