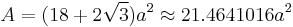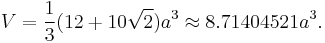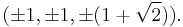Rhombicuboctahedron

Rhombicuboctahedron

(Click here for rotating model)
Type Archimedean solid
Uniform polyhedron
Elements F = 26, E = 48, V = 24 (χ = 2)
Faces by sides 8{3}+(6+12){4}
Schläfli symbol t0,2{4,3}
Wythoff symbol 3 4 | 2
Coxeter-Dynkin
Symmetry Oh, [4,3], (*432)
Dihedral Angle
References U10, C22, W13
Properties Semiregular convex

Colored faces
3.4.4.4
(Vertex figure)

Deltoidal icositetrahedron
(dual polyhedron)
Net

In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles while the other twelve share an edge. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

The name rhombicuboctahedron refers to the fact that 12 of the square faces lie in the same planes as the 12 faces of the rhombic dodecahedron which is dual to the cuboctahedron. Great rhombicuboctahedron is an alternative name for a truncated cuboctahedron, whose faces are parallel to those of the (small) rhombicuboctahedron.

It can also be called an expanded cube or cantellated cube or a cantellated octahedron from truncation operations of the uniform polyhedron.

If the original rhombicuboctahedron has unit edge length, its dual strombic icositetrahedron has edge lengths

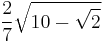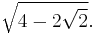
\frac{2}{7}\sqrt{10-\sqrt{2}} and \sqrt{4-2\sqrt{2}}.\

Contents

Area and volume

The area A and the volume V of the rhombicuboctahedron of edge length a are:

A = (18%2B2\sqrt{3})a^2 \approx 21.4641016a^2
V = \frac{1}{3} (12%2B10\sqrt{2})a^3 \approx 8.71404521a^3.

Cartesian coordinates

Orthographic projections

Cartesian coordinates for the vertices of a rhombicuboctahedron centred at the origin, with edge length 2 units, are all permutations of

(\pm1, \pm1, \pm(1%2B\sqrt{2})).\

Geometric relations

There are three pairs of parallel planes that each intersect the rhombicuboctahedron in a regular octagon. The rhombicuboctahedron may be divided along any of these to obtain an octagonal prism with regular faces and two additional polyhedra called square cupolae, which count among the Johnson solids; it is thus an elongated square orthobicupola. These pieces can be reassembled to give a new solid called the elongated square gyrobicupola or pseudorhombicuboctahedron, with the symmetry of a square antiprism. In this the vertices are all locally the same as those of a rhombicuboctahedron, with one triangle and three squares meeting at each, but are not all identical with respect to the entire polyhedron, since some are closer to the symmetry axis than others.

Rhombicuboctahedron
Pseudorhombicuboctahedron

There are distortions of the rhombicuboctahedron that, while some of the faces are not regular polygons, are still vertex-uniform. Some of these can be made by taking a cube or octahedron and cutting off the edges, then trimming the corners, so the resulting polyhedron has six square and twelve rectangular faces. These have octahedral symmetry and form a continuous series between the cube and the octahedron, analogous to the distortions of the rhombicosidodecahedron or the tetrahedral distortions of the cuboctahedron. However, the rhombicuboctahedron also has a second set of distortions with six rectangular and sixteen trapezoidal faces, which do not have octahedral symmetry but rather Th symmetry, so they are invariant under the same rotations as the tetrahedron but different reflections.

The lines along which a Rubik's Cube can be turned are, projected onto a sphere, similar, topologically identical, to a rhombicuboctahedron's edges. In fact, variants using the Rubik's Cube mechanism have been produced which closely resemble the rhombicuboctahedron.

The rhombicuboctahedron is used in three uniform space-filling tessellations: the cantellated cubic honeycomb, the runcitruncated cubic honeycomb, and the runcinated alternated cubic honeycomb.

It shares its vertex arrangement with three nonconvex uniform polyhedra: the stellated truncated hexahedron, the small rhombihexahedron (having the triangular faces and 6 square faces in common), and the small cubicuboctahedron (having 12 square faces in common).


Rhombicuboctahedron
Small cubicuboctahedron
Small rhombihexahedron
Stellated truncated hexahedron

In the arts

The polyhedron in the portrait of Luca Pacioli is a glass rhombicuboctahedron half-filled with water.

A spherical 180x360° panorama can be projected onto any polyhedron; but the rhombicuboctahedron provides a good enough approximation of a sphere while being easy to build. This type of projection, called 'Philosphere', is possible from some panorama assembly software. It consists of two images that are printed separately and cut with scissors while leaving some flaps for assembly with glue.[1]

Games and toys

The Freescape games Driller and Dark Side both had a game map in the form of a rhombicuboctahedron.

A level in the videogame Super Mario Galaxy has a planet in the shape of a rhombicuboctahedron.

During the Rubik's Cube craze of the 1980s, one combinatorial puzzle sold had the form of a rhombicuboctahedron (the mechanism was of course that of a Rubik's Cube).

The Rubik's Snake toy was usually sold in the shape of a stretched rhombicuboctahedron (12 of the squares being replaced with 1:√2 rectangles).

See also

Notes

  1. ^ Philosphere

References

External links

Platonic solids (regular)
Archimedean solids
(Semiregular/Uniform)
Catalan solids
(Dual semiregular)
Dihedral regular
Dihedral uniform
Duals of dihedral uniform
Dihedral others
Degenerate polyhedra are in italics.