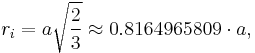Rhombic dodecahedron

Rhombic dodecahedron
(Click here for rotating model)
Type	Catalan solid
Face type	rhombus
Faces	12
Edges	24
Vertices	14
Vertices by type	8{3}+6{4}
Face configuration	V3.4.3.4
Symmetry group	O_h, [4,3], *432
Dihedral angle	120°
Properties	convex, face-transitive edge-transitive, zonohedron
Cuboctahedron (dual polyhedron)	Net

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.

1 Properties
2 Dimensions
3 Area and volume
4 Cartesian coordinates
5 Related polyhedra
- 5.1 Stellation
6 Honeycomb
7 Related polytopes
8 See also
9 References
10 External links

Properties

The rhombic dodecahedron is a zonohedron. Its polyhedral dual is the cuboctahedron. The long diagonal of each face is exactly √2 times the length of the short diagonal, so that the acute angles on each face measure cos⁻¹(1/3), or approximately 70.53°.

Being the dual of an Archimedean polyhedron, the rhombic dodecahedron is face-transitive, meaning the symmetry group of the solid acts transitively on the set of faces. In elementary terms, this means that for any two faces A and B there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B.

The rhombic dodecahedron is one of the nine edge-transitive convex polyhedra, the others being the five Platonic solids, the cuboctahedron, the icosidodecahedron and the rhombic triacontahedron.

The rhombic dodecahedron can be used to tessellate 3-dimensional space. It can be stacked to fill a space much like hexagons fill a plane.

This tessellation can be seen as the Voronoi tessellation of the face-centred cubic lattice. Some minerals such as garnet form a rhombic dodecahedral crystal habit. Honeybees use the geometry of rhombic dodecahedra to form honeycomb from a tessellation of cells each of which is a hexagonal prism capped with half a rhombic dodecahedron. The rhombic dodecahedron also appears in the unit cells of diamond and diamondoids. In these cases, four vertices are absent, but the chemical bonds lie on the remaining edges.^[1]

Dimensions

If the edge length of a rhombic dodecahedron is a, the radius of an inscribed sphere (tangent to each of the rhombic dodecahedron's faces) is

$r_i = a \sqrt{\frac{2}{3}} \approx 0.8164965809 \cdot a,$

the radius of the midsphere is

$r_m = a \frac23 \sqrt{2} \approx 0.94280904158 \cdot a,$ .

and the radius of the circumscribed sphere is

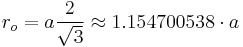$r_o = a \frac2{\sqrt{3}} \approx 1.154700538 \cdot a$ .

Area and volume

The area A and the volume V of the rhombic dodecahedron of edge length a are:

$A = 8\sqrt{2}a^2 \approx 11.3137085a^2$

$V = \frac{16}{9} \sqrt{3}a^3 \approx 3.07920144a^3$

Cartesian coordinates

The eight vertices where three faces meet at their obtuse angles have Cartesian coordinates:

(±1, ±1, ±1)

The coordinates of the six vertices where four faces meet at their acute angles are the permutations of:

(0, 0, ±2)

Related polyhedra

This polyhedron is a part of a sequence of rhombic polyhedra and tilings with [n,3] Coxeter group symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are squares.

Polyhedra			Euclidean tiling	Hyperbolic tiling
[3,3]	[4,3]	[5,3]	[6,3]	[7,3]	[8,3]
Cube	Rhombic dodecahedron	Rhombic triacontahedron	Rhombille

Similarly it relates to the infinite series of tilings with the face configurations V3.2n.3.2n, the first in the Euclidean plane, and the rest in the hyperbolic plane.

V3.4.3.4 (Drawn as a net)	V3.6.3.6 Euclidean plane tiling Rhombille tiling	V3.8.3.8 Hyperbolic plane tiling (Drawn in a Poincaré disk model)

Stellation

The stellated rhombic dodecahedron can be seen as a rhombic dodecahedron with rhombic-based pyramids augmented to each face, with a pyramid height extending the face planes of the neighboring faces:

Honeycomb

The rhombic dodecahedron can tessellate space by translational copies of itself:

Related polytopes

The rhombic dodecahedron forms the hull of the vertex-first projection of a tesseract to 3 dimensions. There are exactly two ways of decomposing a rhombic dodecahedron into 4 congruent parallelepipeds, giving 8 possible parallelepipeds. The 8 cells of the tesseract under this projection map precisely to these 8 parallelepipeds.

The rhombic dodecahedron forms the maximal cross-section of a 24-cell, and also forms the hull of its vertex-first parallel projection into 3 dimensions. The rhombic dodecahedron can be decomposed into 6 congruent (but non-regular) square dipyramids meeting at a single vertex in the center; these form the images of 6 pairs of the 24-cell's octahedral cells. The remaining 12 octahedral cells project onto the faces of the rhombic dodecahedron. The non-regularity of these images are due to projective distortion; the facets of the 24-cell are regular octahedra in 4-space.

This decomposition gives an interesting method for constructing the rhombic dodecahedron: cut a cube into 6 congruent square pyramids, and attach them to the faces of a second cube. The triangular faces of each pair of adjacent pyramids lie on the same plane, and so merge into rhombuses. The 24-cell may also be constructed in an analogous way using two tesseracts.

References

^ Dodecahedral Crystal Habit

Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 730208, http://books.google.com/?id=mfmzUjhs-_8C&pg=PA19 (The thirteen semiregular convex polyhedra and their duals, Page 19, Rhombic dodecahedron)
The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 285, Rhombic dodecahedron )

External links

Eric W. Weisstein, Rhombic dodecahedron (Catalan solid) at MathWorld.
Virtual Reality Polyhedra – The Encyclopedia of Polyhedra

Computer models

Rhombic Dodecahedron -- interactive 3-d model
Relating a Rhombic Triacontahedron and a Rhombic Dodecahedron, Rhombic Dodecahedron 5-Compound and Rhombic Dodecahedron 5-Compound by Sándor Kabai, The Wolfram Demonstrations Project.

Paper projects

Rhombic Dodecahedron Calendar – make a rhombic dodecahedron calendar without glue
Another Rhombic Dodecahedron Calendar – made by plaiting paper strips

Practical applications

Archimede Institute Examples of actual housing construction projects using this geometry

Polyhedron navigator

Platonic solids (regular)	tetrahedron · cube · octahedron · dodecahedron · icosahedron

Archimedean solids (Semiregular/Uniform)	truncated tetrahedron · cuboctahedron · truncated cube · truncated octahedron · rhombicuboctahedron · truncated cuboctahedron · snub cube · icosidodecahedron · truncated dodecahedron · truncated icosahedron · rhombicosidodecahedron · truncated icosidodecahedron · snub dodecahedron

Catalan solids (Dual semiregular)	triakis tetrahedron · rhombic dodecahedron · triakis octahedron · tetrakis cube · deltoidal icositetrahedron · disdyakis dodecahedron · pentagonal icositetrahedron · rhombic triacontahedron · triakis icosahedron · pentakis dodecahedron · deltoidal hexecontahedron · disdyakis triacontahedron · pentagonal hexecontahedron

Dihedral regular	dihedron · hosohedron

Dihedral uniform	prisms · antiprisms

Duals of dihedral uniform	bipyramids · trapezohedra

Dihedral others	pyramids · truncated trapezohedra · gyroelongated bipyramid · cupola · bicupola · pyramidal frusta

Degenerate polyhedra are in italics.