Rheonomous

A mechanical system is rheonomous if the equations of constraints contain the time as an explicit variable.[1] Such constraints are called rheonomic constraints.

Example: pendulum

As shown at right, a simple pendulum is a system composed of a weight and a string. The string is attached at the top end to a pivot and at the bottom end to a weight. Being inextensible, the string’s length is a constant. Therefore, this system is scleronomous; it obeys scleronomic constraint

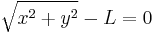\sqrt{x^2%2By^2} - L=0\,\! ,

where 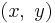(x,\ y)\,\! is the position of the weight and 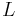L\,\! is length of the string.

Refer to figure at right, Assume the top end of the string is attached to a pivot point undergoing a simple harmonic motion

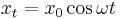x_t=x_0\cos\omega t\,\! ,

where 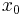x_0\,\! is amplitude, 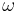\omega\,\! is angular frequency, and 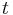t\,\! is time.

Although the top end of the string is not fixed, the length of this inextensible string is still a constant. The distance between the top end and the weight must stay the same. Therefore, this system is a rheonomous; it obeys rheonomic constraint

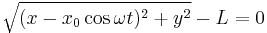\sqrt{(x - x_0\cos\omega t)^2%2By^2} - L=0\,\! .

See also

References

  1. ^ Goldstein, Herbert (1980). Classical Mechanics (3rd ed.). United States of America: Addison Wesley. p. 13. ISBN 0201657023.