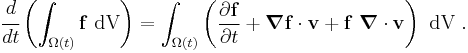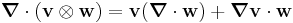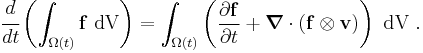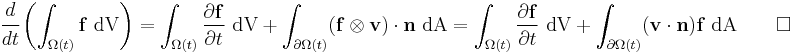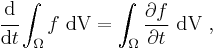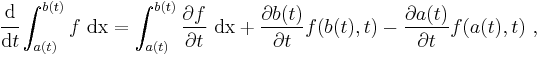Reynolds transport theorem
Reynolds' transport theorem (also known as the Leibniz-Reynolds' transport theorem), or in short Reynolds theorem, is a three-dimensional generalization of the Leibniz integral rule which is also known as differentiation under the integral sign. The theorem is named after Osborne Reynolds (1842–1912). It is used to recast derivatives of integrated quantities and is useful in formulating the basic equations of continuum mechanics.
Consider integrating 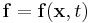 over the time-dependent region
over the time-dependent region 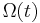 that has boundary
that has boundary 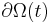 , then taking the derivative with respect to time:
, then taking the derivative with respect to time:
If we wish to move the derivative under the integral sign there are two issues: the time dependence of 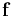 , and the introduction of and removal of space from
, and the introduction of and removal of space from  due to its dynamic boundary. Reynolds' transport theorem provides the necessary framework.
due to its dynamic boundary. Reynolds' transport theorem provides the necessary framework.
Contents |
General form
Reynolds' transport theorem, derived in [1] [2], is:
in which 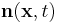 is the outward-pointing unit-normal,
is the outward-pointing unit-normal, 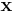 is a point in the region and is the variable of integration,
is a point in the region and is the variable of integration, 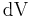 and
and 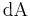 are volume and surface elements at
are volume and surface elements at 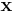 , and
, and 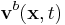 is the velocity of the area element. The function
is the velocity of the area element. The function 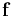 may be vector or scalar valued. Note that the integral on the left hand side is a function solely of time, and so the total derivative has been used.
may be vector or scalar valued. Note that the integral on the left hand side is a function solely of time, and so the total derivative has been used.
Form for a Material Element
In continuum mechanics this theorem is often used for material elements, which are parcels of fluids or solids which no material enters or leaves. If 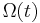 is a material element then there is a velocity function
is a material element then there is a velocity function 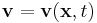 and the boundary elements obey
and the boundary elements obey
This condition may be substituted to obtain [3]
-
Proof for a Material Element Let
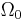 be reference configuration of the region
be reference configuration of the region 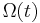 . Let the motion and the deformation gradient be given by
. Let the motion and the deformation gradient be given byLet
![J(\mathbf{X},t) = \det[\boldsymbol{F}(\mathbf{X},t)]](/2012-wikipedia_en_all_nopic_01_2012/I/86260e5678fc36761f786c382a34f898.png) . Then, integrals in the current and the reference configurations are related by
. Then, integrals in the current and the reference configurations are related byThat this derivation is for a material element is implicit in the time constancy of the reference configuration: it is constant in material coordinates. The time derivative of an integral over a volume is defined as
Converting into integrals over the reference configuration, we get
Since
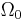 is independent of time, we have
is independent of time, we haveNow, the time derivative of
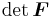 is given by [4]
is given by [4]Therefore,
where
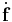 is the material time derivative of
is the material time derivative of 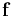 . Now, the material derivative is given by
. Now, the material derivative is given byTherefore,
or,
Using the identity
we then have
Using the divergence theorem and the identity
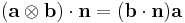 we have
we have
Erroneous sources
This theorem is widely quoted, incorrectly, as being the form specific to material volumes. See the planetmath external link below for an example. Clearly, if the material volume form is applied to regions other than material volumes, errors will ensue.
A special case
If we take  to be constant with respect to time, then
to be constant with respect to time, then 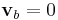 and the identity reduces to
and the identity reduces to
as expected. This simplification is not possible if an incorrect form of the Reynolds transport theorem is used.
Interpretation and reduction to one dimension
The theorem is the higher dimensional extension of Differentiation under the integral sign and should reduce to that expression in some cases. Suppose  is independent of
is independent of  &
&  , and that
, and that 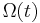 is a unit square in the
is a unit square in the 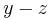 plane and has
plane and has  limits
limits 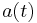 and
and 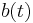 . Then Reynolds transport theorem reduces to
. Then Reynolds transport theorem reduces to
which is the expression given on Differentiation under the integral sign, except that there the variables x and t have been swapped.
See also
Notes
- ^ L. G. Leal, 2007, p. 23.
- ^ O. Reynolds, 1903, Vol. 3, p. 14
- ^ T. Belytschko, W. K. Liu, and B. Moran, 2000, Nonlinear Finite Elements for Continua and Structures, John Wiley and Sons, Ltd., New York.
- ^ Gurtin M. E., 1981, An Introduction to Continuum Mechanics. Academic Press, New York, p. 77.
References
L. G. Leal, 2007, Advanced transport phenomena: fluid mechanics and convective transport processes, Cambridge University Press, p. 912.
O. Reynolds, 1903, Papers on Mechanical and Physical Subjects, Vol. 3, The Sub-Mechanics of the Universe, Cambridge University Press, Cambridge.
External links
- Osborne Reynolds, Collected Papers on Mechanical and Physical Subjects, in three volumes, published circa 1903, now fully and freely available in digital format:
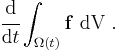
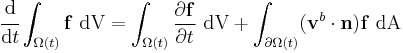
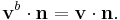
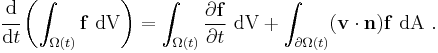
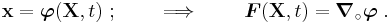
![\int_{\Omega(t)} \mathbf{f}(\mathbf{x},t)~\text{dV} =
\int_{\Omega_0} \mathbf{f}[\boldsymbol{\varphi}(\mathbf{X},t),t]~J(\mathbf{X},t)~\text{dV}_0 =
\int_{\Omega_0} \hat{\mathbf{f}}(\mathbf{X},t)~J(\mathbf{X},t)~\text{dV}_0 ~.](/2012-wikipedia_en_all_nopic_01_2012/I/6b7ed02827498b2dbe7342fcb16aa68a.png)
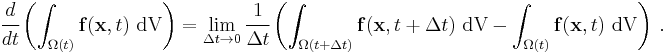
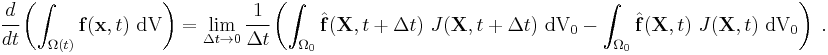
![\begin{align}
\cfrac{d}{dt}\left( \int_{\Omega(t)} \mathbf{f}(\mathbf{x},t)~\text{dV}\right) & =
\int_{\Omega_0} \left[\lim_{\Delta t \rightarrow 0} \cfrac{
\hat{\mathbf{f}}(\mathbf{X},t%2B\Delta t)~J(\mathbf{X},t%2B\Delta t) -
\hat{\mathbf{f}}(\mathbf{X},t)~J(\mathbf{X},t)}{\Delta t} \right]~\text{dV}_0 \\
& = \int_{\Omega_0} \frac{\partial }{\partial t}[\hat{\mathbf{f}}(\mathbf{X},t)~J(\mathbf{X},t)]~\text{dV}_0 \\
& = \int_{\Omega_0} \left(
\frac{\partial }{\partial t}[\hat{\mathbf{f}}(\mathbf{X},t)]~J(\mathbf{X},t)%2B
\hat{\mathbf{f}}(\mathbf{X},t)~\frac{\partial }{\partial t}[J(\mathbf{X},t)]\right) ~\text{dV}_0
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/3bde5047de442befcd9dc185f08c26f0.png)
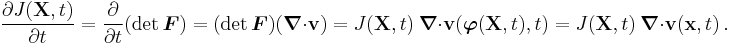
![\begin{align}
\cfrac{d}{dt}\left( \int_{\Omega(t)} \mathbf{f}(\mathbf{x},t)~\text{dV}\right) & =
\int_{\Omega_0} \left(
\frac{\partial }{\partial t}[\hat{\mathbf{f}}(\mathbf{X},t)]~J(\mathbf{X},t)%2B
\hat{\mathbf{f}}(\mathbf{X},t)~J(\mathbf{X},t)~\boldsymbol{\nabla} \cdot \mathbf{v}(\mathbf{x},t)\right) ~\text{dV}_0 \\
& =
\int_{\Omega_0}
\left(\frac{\partial }{\partial t}[\hat{\mathbf{f}}(\mathbf{X},t)]%2B
\hat{\mathbf{f}}(\mathbf{X},t)~\boldsymbol{\nabla} \cdot \mathbf{v}(\mathbf{x},t)\right)~J(\mathbf{X},t) ~\text{dV}_0 \\
& =
\int_{\Omega(t)}
\left(\dot{\mathbf{f}}(\mathbf{x},t)%2B
\mathbf{f}(\mathbf{x},t)~\boldsymbol{\nabla} \cdot \mathbf{v}(\mathbf{x},t)\right)~\text{dV}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/b4e7aac62c78aa61f7811b42e283b1d0.png)
![\dot{\mathbf{f}}(\mathbf{x},t) =
\frac{\partial \mathbf{f}(\mathbf{x},t)}{\partial t} %2B [\boldsymbol{\nabla} \mathbf{f}(\mathbf{x},t)]\cdot\mathbf{v}(\mathbf{x},t) ~.](/2012-wikipedia_en_all_nopic_01_2012/I/5c05c282a558a9ce7dd4f17ec271c626.png)
![\cfrac{d}{dt}\left( \int_{\Omega(t)} \mathbf{f}(\mathbf{x},t)~\text{dV}\right) =
\int_{\Omega(t)}
\left(
\frac{\partial \mathbf{f}(\mathbf{x},t)}{\partial t} %2B [\boldsymbol{\nabla} \mathbf{f}(\mathbf{x},t)]\cdot\mathbf{v}(\mathbf{x},t) %2B
\mathbf{f}(\mathbf{x},t)~\boldsymbol{\nabla} \cdot \mathbf{v}(\mathbf{x},t)\right)~\text{dV}](/2012-wikipedia_en_all_nopic_01_2012/I/f1a4f88166e8f0c07a1bc8d93affef7b.png)